A coin is tossed 4 times. Find the mean and variance of the probability distribution of the number of tails.
The correct Answer is:Mean = 2 and variance = 1
To find the mean and variance of the probability distribution of the number of tails when a coin is tossed 4 times, we can follow these steps:
Step 1: Identify the parameters
In this problem, we have:
- Number of trials (n) = 4 (since the coin is tossed 4 times)
- Probability of getting tails (P) = 1/2
- Probability of getting heads (Q) = 1 - P = 1/2
Step 2: Calculate the Mean
The mean (μ) of a binomial distribution can be calculated using the formula:
μ=n⋅P
Substituting the values:
μ=4⋅12=2
Step 3: Calculate the Variance
The variance (σ²) of a binomial distribution can be calculated using the formula:
σ2=n⋅P⋅Q
Substituting the values:
σ2=4⋅12⋅12=4⋅14=1
Final Results
- Mean (μ) = 2
- Variance (σ²) = 1
In this problem, we have:
- Number of trials (n) = 4 (since the coin is tossed 4 times)
- Probability of getting tails (P) = 1/2
- Probability of getting heads (Q) = 1 - P = 1/2
The mean (μ) of a binomial distribution can be calculated using the formula:
μ=n⋅P
Substituting the values:
μ=4⋅12=2
The variance (σ²) of a binomial distribution can be calculated using the formula:
σ2=n⋅P⋅Q
Substituting the values:
σ2=4⋅12⋅12=4⋅14=1
- Mean (μ) = 2
- Variance (σ²) = 1
Topper's Solved these Questions
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:FOUR MARK QUESTIONS
Explore 9 Videos
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:SIX MARK QUESTIONS
Explore 20 Videos
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:SIX MARK QUESTIONS
Explore 20 Videos
- PRACTICE PAPER IIIBook:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER IIIExercise:Section D
Explore 6 Videos
- RELATIONS AND FUNCTIONS Book:CBSE COMPLEMENTARY MATERIALChapter:RELATIONS AND FUNCTIONS Exercise:SIX MARK QUESTIONS
Explore 7 Videos
Similar Questions
Knowledge Check
Three coins are tossed. Then the probability distribution of number of head is
A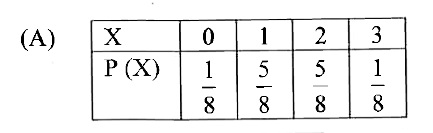 B
B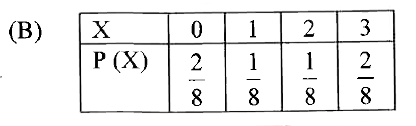 C
C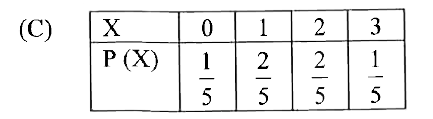 D
D
A coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed three times, find the probability distribution of number of tails.
View SolutionA coin is tossed 4 times . If x is the number of heads observed , find the probability distribution of X.
View Solution(a) (i) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
(ii) Find the probability distribution of the number of tails in the simultaneous tosses of three coins.
(iii) Find the probability distribution of the number of heads in the simultaneous toss of four coins.
(b) (i) Find the probability distribution of the number of heads in three tosses of a coin.
(ii) Find the probability distribution of the number of sixes in two tosses of a die.
( c ) Find the probability distribution of the number of heads (tails) in four tosses of a coin.
View SolutionA coin is biased so that the head is 3 times as likely to occur as tail. If the coin is tossed twice, find the probability distribution of number of tails.
View SolutionFind the mean and variance of the number of heads in the two tosses of a coin.
View SolutionEight coins are tossed at a time for 256 times. Find the expected frequencies of the distribution of heads and tails and tabulate the result. Calculate the mean number of heads and standard deviation.
View SolutionA coin is tossed until a head appears or the tail appears 4 times in succession. Find the probability distribution of the number of tosses.
View Solution