A coin is tossed 4 times . If x is the number of heads observed , find the probability distribution of X.
To find the probability distribution of the random variable X, which represents the number of heads observed when a coin is tossed 4 times, we can follow these steps:
Step 1: Identify the Random Variable
Let X be the number of heads obtained when a coin is tossed 4 times. The possible values of X are 0,1,2,3, and 4.
Step 2: Determine the Total Number of Outcomes
When a coin is tossed 4 times, the total number of outcomes is given by:
N=2n=24=16
where n is the number of tosses.
Step 3: Calculate the Probability for Each Value of X
We can use the binomial probability formula to find the probability of getting k heads in n tosses:
P(X=k)=(nk)pk(1−p)n−k
where:
- n=4 (number of trials),
- k is the number of heads,
- p=0.5 (probability of getting heads in a single toss).
Now we will calculate P(X=k) for k=0,1,2,3,4.
Step 4: Calculate Each Probability
1. For k=0:
P(X=0)=(40)(0.5)0(0.5)4=1⋅1⋅116=116
2. For k=1:
P(X=1)=(41)(0.5)1(0.5)3=4⋅0.5⋅18=416=14
3. For k=2:
P(X=2)=(42)(0.5)2(0.5)2=6⋅14⋅14=616=38
4. For k=3:
P(X=3)=(43)(0.5)3(0.5)1=4⋅18⋅0.5=416=14
5. For k=4:
P(X=4)=(44)(0.5)4(0.5)0=1⋅116⋅1=116
Step 5: Summarize the Probability Distribution
The probability distribution of X can be summarized as follows:
P(X=0)=116P(X=1)=14=416P(X=2)=38=616P(X=3)=14=416P(X=4)=116
Final Probability Distribution Table
XP(X)01161416261634164116
Let X be the number of heads obtained when a coin is tossed 4 times. The possible values of X are 0,1,2,3, and 4.
When a coin is tossed 4 times, the total number of outcomes is given by:
N=2n=24=16
where n is the number of tosses.
We can use the binomial probability formula to find the probability of getting k heads in n tosses:
P(X=k)=(nk)pk(1−p)n−k
where:
- n=4 (number of trials),
- k is the number of heads,
- p=0.5 (probability of getting heads in a single toss).
P(X=0)=(40)(0.5)0(0.5)4=1⋅1⋅116=116
P(X=1)=(41)(0.5)1(0.5)3=4⋅0.5⋅18=416=14
P(X=2)=(42)(0.5)2(0.5)2=6⋅14⋅14=616=38
P(X=3)=(43)(0.5)3(0.5)1=4⋅18⋅0.5=416=14
P(X=4)=(44)(0.5)4(0.5)0=1⋅116⋅1=116
The probability distribution of X can be summarized as follows:
XP(X)01161416261634164116
Topper's Solved these Questions
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Exercise 31
18 Videos
- PROBABILITY DISTRIBUTIONBOOK - RS AGGARWALCHAPTER - PROBABILITY DISTRIBUTIONEXERCISE - Objective Questions
30 Videos
- PROBABILITYBOOK - RS AGGARWALCHAPTER - PROBABILITYEXERCISE - Exercise 29 B
2 Videos
- PRODUCT OF THREE VECTORSBOOK - RS AGGARWALCHAPTER - PRODUCT OF THREE VECTORSEXERCISE - Objective Questions
34 Videos
Similar Questions
Knowledge Check
A fair coin is tossed 4 times. If X denotes the number of heads obtained, then the formula for p.m.f. of X is
Af(x)={1164Cx,x=0,1,2,3,40, otherwiseBf(x)={184Cx,x=0,1,2,3,40, otherwiseCf(x)={144Cx,x=0,1,2,3,40, otherwiseDf(x)={124Cx,x=0,1,2,3,40, otherwiseThree coins are tossed. Then the probability distribution of number of head is
A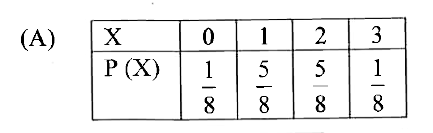 B
B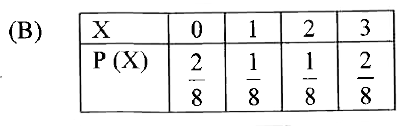 C
C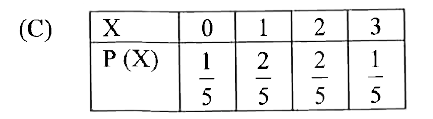 D
D
Three balance coins are tossed simultaneoulsy. If X denotes the number of heads, find probaility distribution of X.
View SolutionA fair coin is tossed four times. Let X denote the number of heads occurring. Find the probability distribution, mean and variance of X.
View SolutionA fair coin is tossed 3 times. Let X be the number of heads obtained. Find E(X) and V(X).
View SolutionA coin is tossed 4 times. Find the mean and variance of the probability distribution of the number of tails.
View SolutionA coin is tossed until a head appears or the tail appears 4 times in succession. Find the probability distribution of the number of tosses.
View Solution(a) (i) Find the probability distribution of the number of heads when three coins are tossed simultaneously.
(ii) Find the probability distribution of the number of tails in the simultaneous tosses of three coins.
(iii) Find the probability distribution of the number of heads in the simultaneous toss of four coins.
(b) (i) Find the probability distribution of the number of heads in three tosses of a coin.
(ii) Find the probability distribution of the number of sixes in two tosses of a die.
( c ) Find the probability distribution of the number of heads (tails) in four tosses of a coin.
View Solution
