The probability distribution of discrete random variable X is given below
x2345P(x)5K7k9k11k
find the value of K.
The correct Answer is:32
To find the value of K in the given probability distribution of the discrete random variable X, we can follow these steps:
Step 1: Write down the probability distribution
The probability distribution is given as:
- P(X=2)=5K
- P(X=3)=7K
- P(X=4)=9K
- P(X=5)=11K
Step 2: Set up the equation for total probability
The sum of all probabilities must equal 1:
P(X=2)+P(X=3)+P(X=4)+P(X=5)=1
Substituting the probabilities:
5K+7K+9K+11K=1
Step 3: Combine the fractions
Since all terms have a common denominator K, we can combine them:
5+7+9+11K=1
Step 4: Calculate the sum of the numerators
Now, calculate the sum of the numerators:
5+7+9+11=32
Step 5: Set up the equation
Now we have:
32K=1
Step 6: Solve for K
To find K, we can rearrange the equation:
32=K
Thus, the value of K is:
K=32
Final Answer
The value of K is 32.
---
The probability distribution is given as:
- P(X=2)=5K
- P(X=3)=7K
- P(X=4)=9K
- P(X=5)=11K
The sum of all probabilities must equal 1:
P(X=2)+P(X=3)+P(X=4)+P(X=5)=1
5K+7K+9K+11K=1
Since all terms have a common denominator K, we can combine them:
5+7+9+11K=1
Now, calculate the sum of the numerators:
5+7+9+11=32
Now we have:
32K=1
To find K, we can rearrange the equation:
32=K
K=32
The value of K is 32.
Topper's Solved these Questions
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:FOUR MARK QUESTIONS
Explore 9 Videos
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:SIX MARK QUESTIONS
Explore 20 Videos
- PROBABILITYBook:CBSE COMPLEMENTARY MATERIALChapter:PROBABILITYExercise:SIX MARK QUESTIONS
Explore 20 Videos
- PRACTICE PAPER IIIBook:CBSE COMPLEMENTARY MATERIALChapter:PRACTICE PAPER IIIExercise:Section D
Explore 6 Videos
- RELATIONS AND FUNCTIONS Book:CBSE COMPLEMENTARY MATERIALChapter:RELATIONS AND FUNCTIONS Exercise:SIX MARK QUESTIONS
Explore 7 Videos
Similar Questions
Knowledge Check
The probability distribution of a discrete random variable X is given below

The value of k isA8B16C32D48If the probability of a random variable X is a given below :
X=x:−2−10123P(X=x):12k152k310k
Then the value of k, is :A110B210C310D710The probability distribution of a random variable X is given as follows:

If E(X)=2.3 , then value of k isA1/2B5/4C3D2
The distribution of a random variable X is goven below
The value of k is

View SolutionThe probability of a random variable X is given below
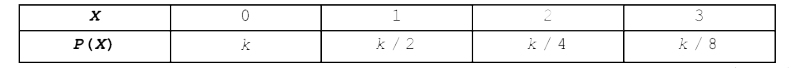
Determine the value of k
View SolutionThe probability distribution of a random variable X is given below: X: 0 1 2 3 P(X):k k2 k4 k8 (i) Determine the value of k (ii) Determine P(X≤2)and P(X>2) (iii) Find P(X≤2)+P(X>2)
View SolutionThe probability distribution of a discrete r. v. X is as follows.

Find the value of k.
View SolutionThe following is the probability distribution of a random vaiable X.
The value of k is
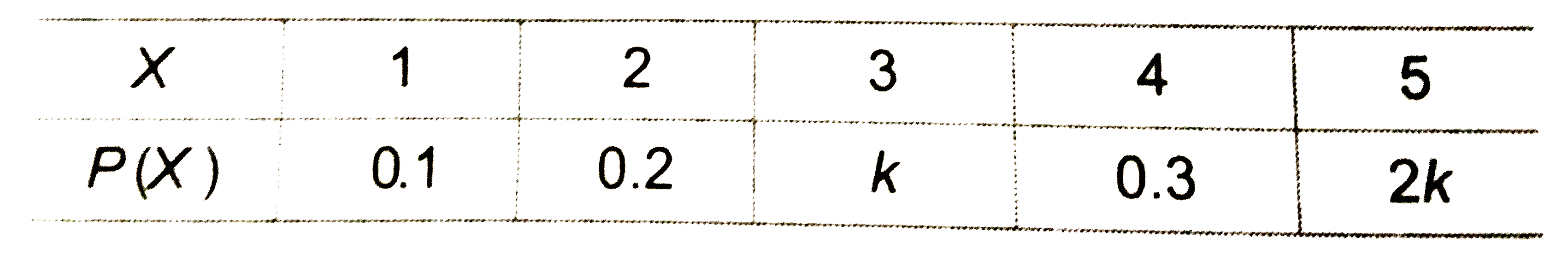
View Solution

