Clamped at the middle a metal rod of length 1 meter and density 7.5gm/cc,gives dust heaps at intervals of 8cm" velocity of sound in the gas used is 400 meter/sec.then the young's modulus of material of the rod will be

Video Solution

Text Solution

Verified by Experts

The situation is shown in figure-6.75.

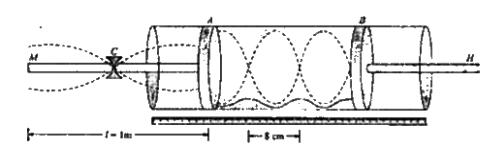
Let $λ_{r}$ and $λ_{g}$ be the wavelength in the rod and gas column respectively. Since the rod is clampted in the middle, it vibrates with a node in the middle and antinodes at the ends. Therefore
$\frac{λ_{r}}{2} = 1 m = 100 c m$
$\frac{λ_{g}}{2} = 8 c m$ If $v_{r}$ and $v_{g}$ be the sound velocities in the rod and in the gas respectively and n be the frequency of vibration, then frequency of oscillations is given as
$n = \frac{v_{r o d}}{λ_{r o d}} = \frac{v_{g a s}}{λ_{g a s}}$
$v_{r o d} = \frac{λ_{r o d}}{λ_{g a s}} \times v_{g a s}$
= $\frac{200}{16} \times 400$
= 5000 m/s
Now velocityof longitudinal waves in a metal rod is given by
$v_{r o d} = \sqrt{(\frac{Y}{d})}$
$Y = v_{r o d}^{2} \times d$
$Y = {(500.0)}^{2} \times 7.5 \times 10^{3}$
= $1.875 \times 10^{11} N / m^{2}$

Updated on:21/07/2023

A metalrod of length 1.5 m is clamed at the centre. When it is set with longitudinal vibratons it emits a note of 1000 Hz. Determine the Young's modulus if the density of material = 8 xx $10^{3}$ $k \frac{g}{m^{3}}$
A $7 \times 10^{10} N / m^{2}$
B $7.2 \times 10^{10} N / m^{2}$
C $0.7 \times 10^{10} N / m^{2}$
D $6.8 \times 10^{10} N / m^{2}$
Standing wave produced in a metal rod of length $1 m$ is represented by the equation $y = 10^{- 6} sin . \frac{π x}{2} sin 200 π t$ where $x$ is in metre and t is in seconds. The maximum tensile stress at the mid point of the rod is (Young's modulus of material of rod $= 10^{12} N / m^{2}$ )
A $\frac{π}{2} \times 10^{6} N / m^{2}$
B $2 π \times 10^{6} N / m^{2}$
C $\frac{π}{2 \sqrt{2}} \times 10^{6} N / m^{2}$
D $\frac{2 π}{\sqrt{3}} \times 10^{6} N / m^{2}$
A $5 k g$ rod of square cross section $5 c m$ on a side and $1 m$ long is pulled along a smooth horizontal surface by a force applied at one end. The rod has a constant acceleration of $2 m s^{- 12}$ . Determine the elongation in the rod. (Young's modulus of the material of the rod is $5 \times 10^{3} N / m^{9}$ ).
AZero, as for elongation to be there, equal and opposite forces must act on the rod
BNon-zero but cannot be determine from the give, situation
C $0.4 μ m$
D $16 μ m$