The density of a uniform steel wire of mass 1.6×10−2kg, and length 2.5 m is 8×103kg/m3. When it is loaded by 8kg, it elongates by 1.25 mm. If g=10m/s2, then the Young's modulus of the material of the wire is
1.5×1011N/m2
2×1011N/m2
1.75×1011N/m2
1.5×1012N/m2
The correct Answer is:B
d=mV=mA×L
∴A=md×L=1.6×10−28×103×2.5=8×10−7m2
∴Y=F×LA×e=8×10×2.58×10−7×1.25×10−3
=2×1011N/m2
Topper's Solved these Questions
- ELASTICITYBook:MARVEL PUBLICATIONChapter:ELASTICITYExercise:Test Your Grasp - 5
Explore 15 Videos
- CURRENT ELECTRICITYBook:MARVEL PUBLICATIONChapter:CURRENT ELECTRICITYExercise:MCQ
Explore 151 Videos
- ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Book:MARVEL PUBLICATIONChapter:ELECTROMAGNETIC INDUCTION AND ALTERNATING CURRENTS Exercise:TEST YOUR GRASP - 16
Explore 30 Videos
Similar Questions
A wire increases by 10−3 of its length when a stress of 1×108Nm−2 is applied to it. What is the Young's modulus of the material of the wire?
View SolutionA body of mass 3.14 kg is suspended from one end of a non uniform wire of length 10m, such that the radius of the wire is changing uniformly from 9.8×10−4 m at one end to 5×10−4 m at the other end. Find the change in length of the wire in mm. Young's modulus of the material of the wire is 2×1011N/m2 (mass of wire is negligible)
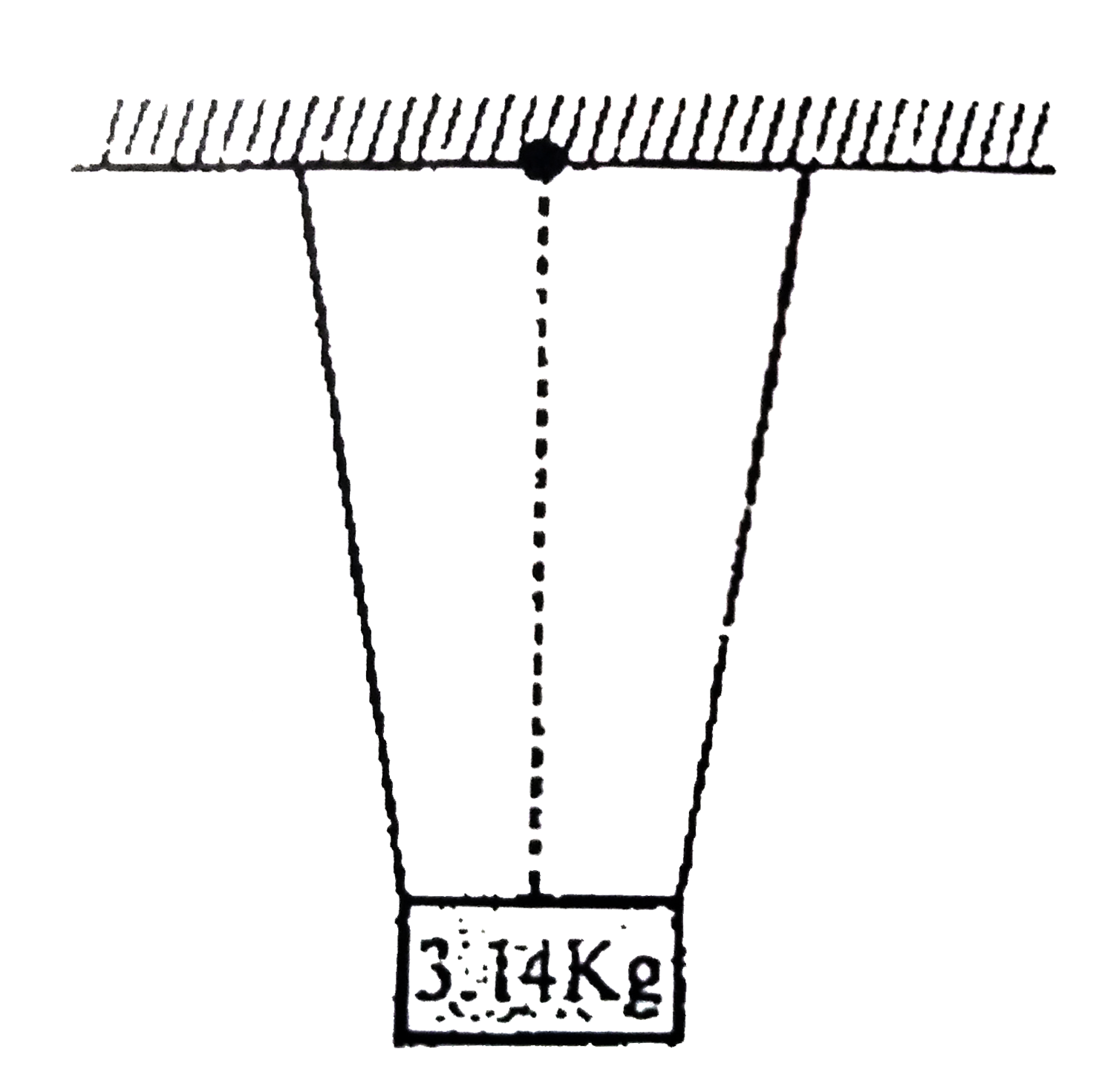
View Solution
Knowledge Check
A load of 3kg produces an extension of 1.5mm in a wire of length 3m and diameter 2mm. Young's modulus of the material of the wire is
A1.87×1010Nm−2B3.5×1010Nm−2C15×1010Nm−2D2.5×1010Nm−2A steel wire of length 1m, and radius 0.1mm is elongated by 1mm due to a weight of 3.14kg. If g=10m/s2, the Young's modulus of the steel wire will be
A8×1011N/m2B1012N/m2C4×1011N/m2D5×1011N/m2A wire of length 10 m and cross-section are 10−6m2 is stretched with a force of 20 N. If the elongation is 1 mm, the Young's modulus of material of the wire will be
A1010N/m2B1011N/m2C2×1010N/m2D2×1011N/m2
When the load on a wire is increased slowly from 4 to 8 kg, the elongation increases from 1.00 mm to 1.6 mm. If g=10m/s2, then the work done during the extention of the wire is
View SolutionWhen a wire 2 m long and 0.05cm2 in cross-section is stretched by a mass of 2 kg, it increases in length by 0.04 mm. Young's modulus of the material of the wire is
(g=10ms−2)
View SolutionA load of 4kg is suspended from a ceiling through a steel wire of length 20m and radius 2mm. It is found that the length of the wire increases by 0.031mm, as equilibrium is achieved. If g=3.1×πms(−2), the value of young's modulus of the material of the wire (in Nm−2) is
View SolutionA uniform steel wire of density 7800kg/m3 is 2.5 m long and weighs 15.6×10−3kg. 2.5 m long and weighs 15.6×10−3 kg . If extends by 1.25 mm when loaded by 8 kg, then the value of Young's modulus for steel will be
View SolutionA block of mass 500kg is suspended by wire of length 70 cm. The area of cross-section of wire is 10 mm2. When the load is removed, the wire contracts by 0.5cm. The young's modulus of the material of wire will be
View Solution

