The speed of longitudinal wave is 100 times, then the speed of transverse wave in a brass wire. What is the stress in wire ? TheYoung's modulus of brass Is 1.0×1011N/m2
The correct Answer is:A, B
To solve the problem, we need to find the stress in the brass wire given that the speed of longitudinal waves is 100 times the speed of transverse waves, and we know the Young's modulus of brass.
1. Define the Variables:
- Let vt be the speed of transverse wave.
- Let vl be the speed of longitudinal wave.
- Given that vl=100×vt.
2. Use the Formula for Wave Speeds:
- The speed of a transverse wave in a wire is given by:
vt=√Tm
where T is the tension in the wire and m is the mass per unit length of the wire.
- The mass per unit length can be expressed as:
m=ρ⋅A
where ρ is the density of the material and A is the cross-sectional area of the wire. For a circular cross-section, A=πr2.
3. Express the Speed of Longitudinal Wave:
- The speed of a longitudinal wave is given by:
vl=√Yρ
where Y is the Young's modulus.
4. Set Up the Relationship:
- From the problem, we know:
vl=100×vt
- Substituting the expressions for vl and vt:
√Yρ=100×√Tρ⋅πr2
5. Square Both Sides:
- Squaring both sides gives:
Yρ=10000×Tρ⋅πr2
6. Cancel ρ:
- Since ρ is on both sides, we can cancel it out:
Y=10000×Tπr2
7. Relate Stress to Young's Modulus:
- Stress σ is defined as:
σ=TA=Tπr2
- Rearranging gives:
T=σ⋅πr2
8. Substitute Back:
- Substitute T back into the equation for Y:
Y=10000×σ⋅πr2πr2
- This simplifies to:
Y=10000σ
9. Solve for Stress:
- Rearranging gives:
σ=Y10000
- Substitute the given value of Young's modulus:
σ=1.0×101110000=1.0×107N/m2
Final Answer:
The stress in the wire is σ=1.0×107N/m2.
---
- Let vt be the speed of transverse wave.
- Let vl be the speed of longitudinal wave.
- Given that vl=100×vt.
- The speed of a transverse wave in a wire is given by:
vt=√Tm
where T is the tension in the wire and m is the mass per unit length of the wire.
- The mass per unit length can be expressed as:
m=ρ⋅A
where ρ is the density of the material and A is the cross-sectional area of the wire. For a circular cross-section, A=πr2.
- The speed of a longitudinal wave is given by:
vl=√Yρ
where Y is the Young's modulus.
- From the problem, we know:
vl=100×vt
- Substituting the expressions for vl and vt:
√Yρ=100×√Tρ⋅πr2
- Squaring both sides gives:
Yρ=10000×Tρ⋅πr2
- Since ρ is on both sides, we can cancel it out:
Y=10000×Tπr2
- Stress σ is defined as:
σ=TA=Tπr2
- Rearranging gives:
T=σ⋅πr2
- Substitute T back into the equation for Y:
Y=10000×σ⋅πr2πr2
- This simplifies to:
Y=10000σ
- Rearranging gives:
σ=Y10000
- Substitute the given value of Young's modulus:
σ=1.0×101110000=1.0×107N/m2
The stress in the wire is σ=1.0×107N/m2.
Topper's Solved these Questions
- WAVES Book:PHYSICS GALAXY - ASHISH ARORAChapter:WAVES Exercise:Advance MCQs with One or More Options Correct
Explore 30 Videos
- WAVE OPTICSBook:PHYSICS GALAXY - ASHISH ARORAChapter:WAVE OPTICSExercise:Unsolved Numerical Problems
Explore 28 Videos
- X-RAYSBook:PHYSICS GALAXY - ASHISH ARORAChapter:X-RAYSExercise:Unsolved Numerica Problem for Preparation
Explore 23 Videos
Similar Questions
The diameter of an iron wire is 1.20 mm. If the speed of transverse waves in the wire is 50.0m/s, what is the tension in the wire? The density of iron is 7.7×103kg/m3
View SolutionA copper wire is held at the two ends by rigid supports. At 30∘C, the wire is just taut, with negligible tension. Find the speed of transverse waves in this wire at 10∘C.
Given : Young modulus of copper =1.3×1011N/m2.
Coefficient of linear expansion of copper =1.7×10−5^(∘)C−1. Density of copper =9×103kg/m3.
View Solution
Knowledge Check
The speed of longitudinal wave is ten times the speed of transverse waves in a tight brass wire. If young's modulus of the wire is Y , then strain in the wire is
A100B1100C110D10In brass the velocity of longitudinal wave is 100 times the velocity of transverse wave if Y=1×1011N/m2, then stress in the wire is
A1×1013Nm−2B1×109Nm−2C1×1011Nm−2D1×107Nm−2If stress is 1012 times the strain produced in a wire, then its Young's modulus will be
A1012 unitsB10−12 unitsC1024 unitsD10−24 units
Two wires of diameter 0.25 cm, one made of steel and the other made of brass are loaded as shown in figure. The unloaded length of steel wire is 1.5 m and that of brass wire is 1.0 m. Compute the elongations of the steel and the brass wires .Young's modulus of steel is 2.0×1011Pa and that of brass is 9.1×1011 Pa.
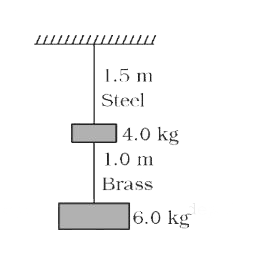
View SolutionThe length of a steel wire is 0.82 m and its mass is 4×10−3 kg. Calculate the speed of transverse waves on the wire if the wire is under a tension of 80 N.
View SolutionHow much force is required to produce an increase of 0.2 % in the length of a brass wire of diameter 0.6 mm
(Young's modulus for brass =0.9×1011N/m2)
View SolutionIf a uniform brass wire of length 5 m and radius 10−3 m is extended by 10−3m, then the energy stored in the wire will be
(Young's modulus for brass =10×1010N/m2)
View SolutionThe time taken by a transverse wave going on a wire having mass 5 g, form one end to another end of wire is 0.5 s. The area of cross-section fo wire is 1mm2 and Young's modulus of elasticity is 16×1011N/m2. The speed of wave is 80 m/s. The strain in wire is
View Solution

