To divide a line segment AB in the ratio 4:7, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1,A2,A3,….. are located at equal distance on the ray AX and the point B is joined to
A12
A11
A10
A9
The correct Answer is:B
(b) Here, minimum 4+7=11 points are located at equal distances on the ray AX, and then B is joined to last point is A11.
Topper's Solved these Questions
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.3 short Answer type Questions
4 Videos
- CONSTRUCTIONSBOOK - NCERT EXEMPLARCHAPTER - CONSTRUCTIONSEXERCISE - Exercise 10.4 Long Answer type Questions
7 Videos
- CIRCLESBOOK - NCERT EXEMPLARCHAPTER - CIRCLESEXERCISE - Circles
44 Videos
- COORDINATE GEOMETRYBOOK - NCERT EXEMPLARCHAPTER - COORDINATE GEOMETRYEXERCISE - Coordinate Geometry
58 Videos
Similar Questions
Divide a line segment AB in the ratio 4:5, a ray AX is drawn first such that ∠BAX is an acute angle and then points A1,A2,A3, ........ are located at equal distances on the ray AX which should be joined to B?
View SolutionTo divide a line segment BC internally in the ratio 3 : 5, we draw a ray BX such that ∠ CBX is an acute angle. What will be the minimum number of points to be located at equal distances, on ray BX?
View Solution
Knowledge Check
To divide a line segment AB in the ratio 5:7, first a ray AX is drawn, so that ∠BAX is an acute angle and then at equal distances point are marked on the ray AX such that the minimum number of these points is
A8B10C11D12To divide a line segment AB in the ratio 2:5, first a ray AX is drawn, so that BAX is an acute angle and then at equal distance points are marked on the ray AX such that the minimum number of these point is:
A2B5C4D7To divide a line segment AB in the ratio 5:6, draw a ray AX such that ∠BAX is an acute angle, the draw a ray BY parallel to AX and the points A1,A2,A3,….. and B1,B2,B3,….. are located to equal distances on ray AX and BY, respectively. Then, the points joined are
AA5 and B6BA6 and B5CA4 and B5DA5 and B4
Divide a line segment AB in the ratio 4:5, the points A1,A2,A3,....andB1,B2,B3,.... are located at equal distances on the ray AX and BY respectively. Which two points should be joined to divide a line segment?
View SolutionDivide a line segment AB in the ratio 3:7, What is the minimum number of points marked on a ray AX at equal distances?
View SolutionTo constuct a triangle similar to a given ΔABC with its sides 73 of the corresponding side of ΔABC, draw a ray BX making acute angle with BC and X lies on the opposite side of A with respect of BC. The points B1,B2,…..,B7 are located at equal distances on BX, B3 is joined to C and then a line segment B6C' is drawn parallel to B3C, where C' lines on BC produced. Finally line segment A'C' is drawn parallel to AC.
View SolutionIn the figure, if B1,B2,B3, and A1,A2,A3,….. have been marked at equal distances. In what ratio C divides AB?
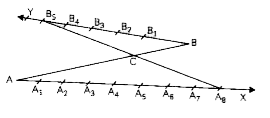
View SolutionThe point which divides the line segment joining the points (7, -6) and (3, 4) in ratio 1 : 2 internally lies in the
View Solution
