Two parallel straight long conducting wires, which are placed at a distance r from each other, are carrying equal currents I in opposite directions. The value of magnetic induction at a point situated at a point situated x from one wire in between the wires will be:
μ0i2π{1r−x−1x}
μ0i2π{1r−x+1x}
μ0i2π(r−x)
μ0i2πx
The correct Answer is:B
To solve the problem of finding the magnetic induction at a point situated at a distance x from one of the two parallel wires carrying equal currents I in opposite directions, we can follow these steps:
Step 1: Understand the Configuration
We have two long parallel wires separated by a distance R. One wire carries current I upwards, and the other wire carries current I downwards. We need to find the magnetic field at a point located x from one wire.
Step 2: Determine the Distances
- The distance from the first wire (the one carrying current I upwards) to the point is x.
- The distance from the second wire (the one carrying current I downwards) to the point is R−x.
Step 3: Calculate the Magnetic Field due to Each Wire
The magnetic field B created by a long straight wire at a distance d from it is given by the formula:
B=μ0I2πd
Magnetic Field due to Wire 1 (upwards current):
B1=μ0I2πx
The direction of B1 is into the page (using the right-hand rule).
Magnetic Field due to Wire 2 (downwards current):
B2=μ0I2π(R−x)
The direction of B2 is also into the page.
Step 4: Find the Net Magnetic Field
Since both magnetic fields B1 and B2 are in the same direction (into the page), we can add them:
Bnet=B1+B2=μ0I2πx+μ0I2π(R−x)
Step 5: Simplify the Expression
Combining the two terms gives:
Bnet=μ0I2π(1x+1R−x)
Final Result
Thus, the value of the magnetic induction at the point situated x from one wire in between the wires is:
Bnet=μ0I2π(1x+1R−x)
We have two long parallel wires separated by a distance R. One wire carries current I upwards, and the other wire carries current I downwards. We need to find the magnetic field at a point located x from one wire.
- The distance from the first wire (the one carrying current I upwards) to the point is x.
- The distance from the second wire (the one carrying current I downwards) to the point is R−x.
The magnetic field B created by a long straight wire at a distance d from it is given by the formula:
B=μ0I2πd
B1=μ0I2πx
The direction of B1 is into the page (using the right-hand rule).
B2=μ0I2π(R−x)
The direction of B2 is also into the page.
Since both magnetic fields B1 and B2 are in the same direction (into the page), we can add them:
Bnet=B1+B2=μ0I2πx+μ0I2π(R−x)
Combining the two terms gives:
Bnet=μ0I2π(1x+1R−x)
Thus, the value of the magnetic induction at the point situated x from one wire in between the wires is:
Bnet=μ0I2π(1x+1R−x)
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-II)
15 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-4 (LEVEL-II)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
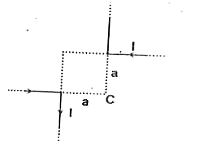
Two inflinitely long wires carrying current I, are bent as shown in the figure. Find the magnetic induction at point C.
View SolutionTwo long parallel wires are separated by a distance of 2m. They carry a current of 1A each in opposite direction. The magnetic induction at the midpoint of a straight line connecting these two wires is
View Solution
Knowledge Check
Two long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
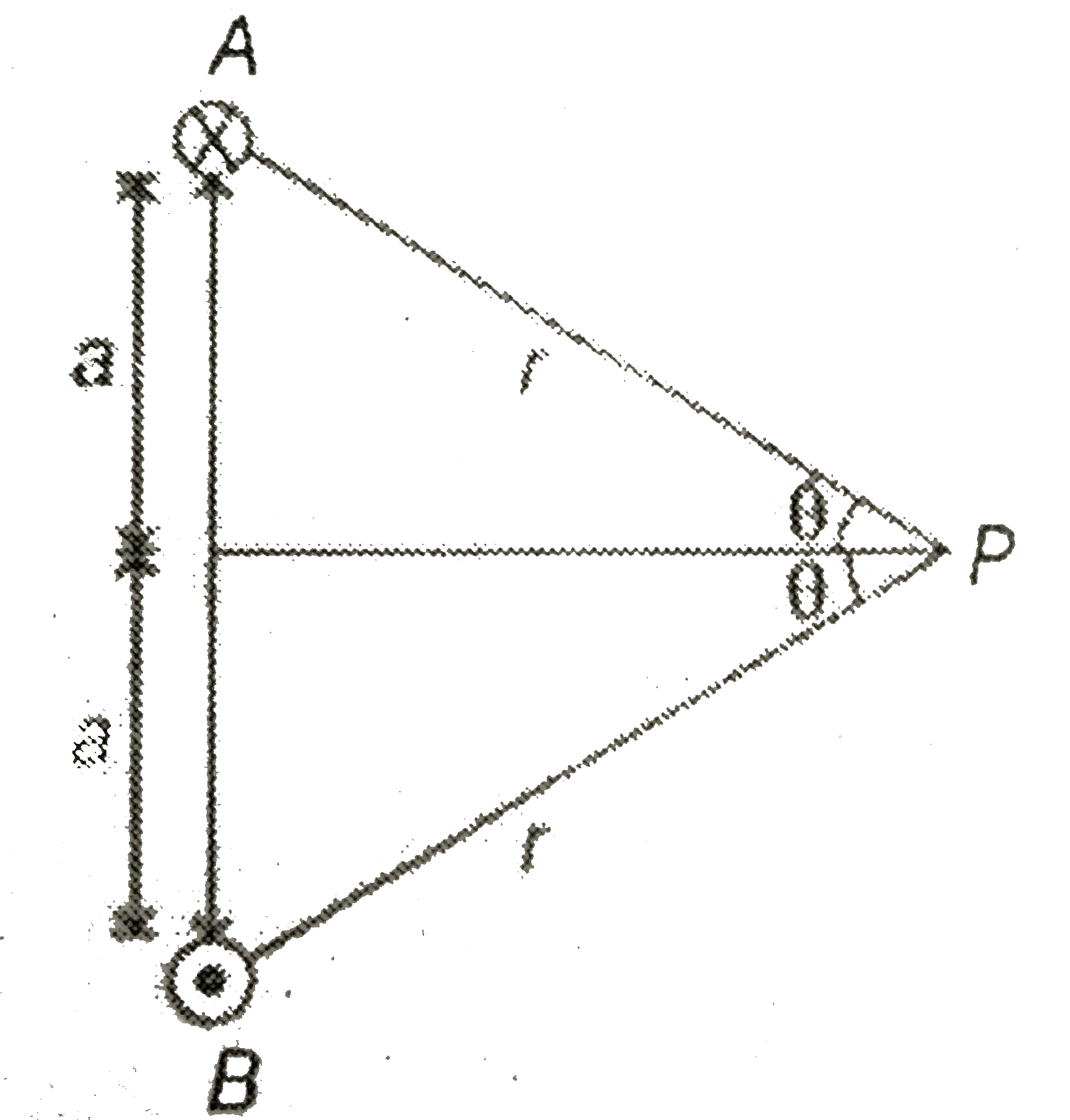 Aμ0la4πr2Bμ0la2πr2Cμ0laπr2Dμ0la√r2−a2πr2
Aμ0la4πr2Bμ0la2πr2Cμ0laπr2Dμ0la√r2−a2πr2The magnetic induction at any point due to a long straight wire carrying a current is
AProportional to the distance from the wireBInversely proportional to the distance from wireCInversely proportional to the square of the distance from the wireDDoes not depend on distanceTwo long straight wires, each carrying a current I in opossite directions asre separated by a distasnce R. The magnetic induction at a point mid way between the wire is
AzeroBμ0IπRC2μIπRDμ0I4πR
Two long straight horizontal parallel wires one above the other are separated by a distance '2a' . If the wires carry equal currents in opposite directions, the magnitude of the magnitude induction in the plane of the wires at a distance 'a' above the upper wire is
View SolutionThe magnetic induction in air at a point 1cm away from a long wire that carries a current of 1A, will be
View SolutionTwo infinitely long parallel wires carry equal current in same direction. The magnetic field at a mid point in between the two wires is
View SolutionThe direction of magnetic field at a point due to an infinitely long wire carrying current is
View SolutionTwo infinitely long parallel wires carry equal currents in the same direction .The magnetic field at a mind point in between the two wires is
View Solution
