Two long straight horizontal parallel wires one above the other are separated by a distance '2a' . If the wires carry equal currents in opposite directions, the magnitude of the magnitude induction in the plane of the wires at a distance 'a' above the upper wire is
μ02πa
μ02πa+μ0i4πa
μ0i2πa−μi4πa
μ0i3πa
The correct Answer is:4
To solve the problem of finding the magnetic induction at a point above the upper wire due to two long straight parallel wires carrying equal currents in opposite directions, we can follow these steps:
1. Identify the Configuration:
- We have two long straight parallel wires, one above the other, separated by a distance of 2a.
- Let the upper wire be Wire 1 and the lower wire be Wire 2.
- The distance from the upper wire to the point of interest (point P) is a.
2. Determine the Magnetic Field due to Wire 1:
- The magnetic field (B1) at a distance a above the upper wire (Wire 1) can be calculated using the formula for the magnetic field around a long straight current-carrying wire:
\(
B_1 = \frac{\mu_0 I}{2 \pi a}
\)
- Here, I is the current flowing through Wire 1, and μ₀ is the permeability of free space.
3. Determine the Magnetic Field due to Wire 2:
- The distance from Wire 2 to point P is 3a (since the total distance between the wires is 2a and point P is a above Wire 1).
- The magnetic field (B2) at point P due to Wire 2 is given by:
\(
B_2 = \frac{\mu_0 I}{2 \pi (3a)}
\)
4. Direction of the Magnetic Fields:
- Since the currents in the two wires are in opposite directions, the magnetic fields will also be in opposite directions.
- Assume that the current in Wire 1 is flowing in the positive direction (creating a magnetic field in one direction), while the current in Wire 2 flows in the opposite direction (creating a magnetic field in the opposite direction).
5. Calculate the Resultant Magnetic Field:
- The resultant magnetic field (B) at point P is the difference between B1 and B2:
\(
B = B_1 - B_2
\)
- Substitute the expressions for B1 and B2:
\(
B = \frac{\mu_0 I}{2 \pi a} - \frac{\mu_0 I}{2 \pi (3a)}
\)
6. Simplify the Expression:
- Factor out the common terms:
\(
B = \frac{\mu_0 I}{2 \pi a} \left(1 - \frac{1}{3}\right)
\)
- Simplifying the term in parentheses:
\(
1 - \frac{1}{3} = \frac{2}{3}
\)
- Thus, we have:
\(
B = \frac{\mu_0 I}{2 \pi a} \cdot \frac{2}{3} = \frac{\mu_0 I}{3 \pi a}
\)
7. Final Result:
- The magnitude of the magnetic induction at a distance a above the upper wire is:
\(
B = \frac{\mu_0 I}{3 \pi a}
\)
Conclusion:
The final answer is:
\(
\text{Magnitude of magnetic induction} = \frac{\mu_0 I}{3 \pi a}
\)
- We have two long straight parallel wires, one above the other, separated by a distance of 2a.
- Let the upper wire be Wire 1 and the lower wire be Wire 2.
- The distance from the upper wire to the point of interest (point P) is a.
- The magnetic field (B1) at a distance a above the upper wire (Wire 1) can be calculated using the formula for the magnetic field around a long straight current-carrying wire:
\(
B_1 = \frac{\mu_0 I}{2 \pi a}
\)
- Here, I is the current flowing through Wire 1, and μ₀ is the permeability of free space.
- The distance from Wire 2 to point P is 3a (since the total distance between the wires is 2a and point P is a above Wire 1).
- The magnetic field (B2) at point P due to Wire 2 is given by:
\(
B_2 = \frac{\mu_0 I}{2 \pi (3a)}
\)
- Since the currents in the two wires are in opposite directions, the magnetic fields will also be in opposite directions.
- Assume that the current in Wire 1 is flowing in the positive direction (creating a magnetic field in one direction), while the current in Wire 2 flows in the opposite direction (creating a magnetic field in the opposite direction).
- The resultant magnetic field (B) at point P is the difference between B1 and B2:
\(
B = B_1 - B_2
\)
- Substitute the expressions for B1 and B2:
\(
B = \frac{\mu_0 I}{2 \pi a} - \frac{\mu_0 I}{2 \pi (3a)}
\)
- Factor out the common terms:
\(
B = \frac{\mu_0 I}{2 \pi a} \left(1 - \frac{1}{3}\right)
\)
- Simplifying the term in parentheses:
\(
1 - \frac{1}{3} = \frac{2}{3}
\)
- Thus, we have:
\(
B = \frac{\mu_0 I}{2 \pi a} \cdot \frac{2}{3} = \frac{\mu_0 I}{3 \pi a}
\)
- The magnitude of the magnetic induction at a distance a above the upper wire is:
\(
B = \frac{\mu_0 I}{3 \pi a}
\)
The final answer is:
\(
\text{Magnitude of magnetic induction} = \frac{\mu_0 I}{3 \pi a}
\)
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:LEVEL-I(C.W)
Explore 58 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:Level-II(C.W)
Explore 63 Videos
- MOVING CHARGES AND MAGNETISMBook:NARAYNAChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE - 4
Explore 20 Videos
- MAGNETISM AND MATTERBook:NARAYNAChapter:MAGNETISM AND MATTERExercise:EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
Explore 17 Videos
- NUCLEAR PHYSICSBook:NARAYNAChapter:NUCLEAR PHYSICSExercise:LEVEL-II-(H.W)
Explore 9 Videos
Similar Questions
Two infinite long straight parallel wires A and B are separted by 0.1m distance and carry equal currents in opposite directions. A square loop of wire C of side 0.1m lies in the plane of A and B. The loop of wire C is kept parallel to both A and B at a distance of 0.1m from the nearest wire. Calculate the EMF induced in the loop C while the currents in A and B are increasing at the rate of 103A/s. Also indicate the direction of current in the loop C.
View SolutionTwo free parallel wires carrying currents in opposite directions
View Solution
Knowledge Check
Two free parallel wires carrying currents in opposite directions
Ado not affect each otherBattract each otherCrepel each otherDnone of theseTwo free parallel wires carrying currents in opposite directions
Arepel each otherBattract each otherCneither attract nor repelDmay attract as well as repel under different values of currents.Two free parallel wires carrying currents in opposite directions
Arepel each otherBattract each otherCneither attract nor repelDmay attract as well as repel under different values of currents
Two free parallel wires carrying currents in opposite directions
View SolutionTwo long parallel wires are separated by a distance of 2m. They carry a current of 1A each in opposite direction. The magnetic induction at the midpoint of a straight line connecting these two wires is
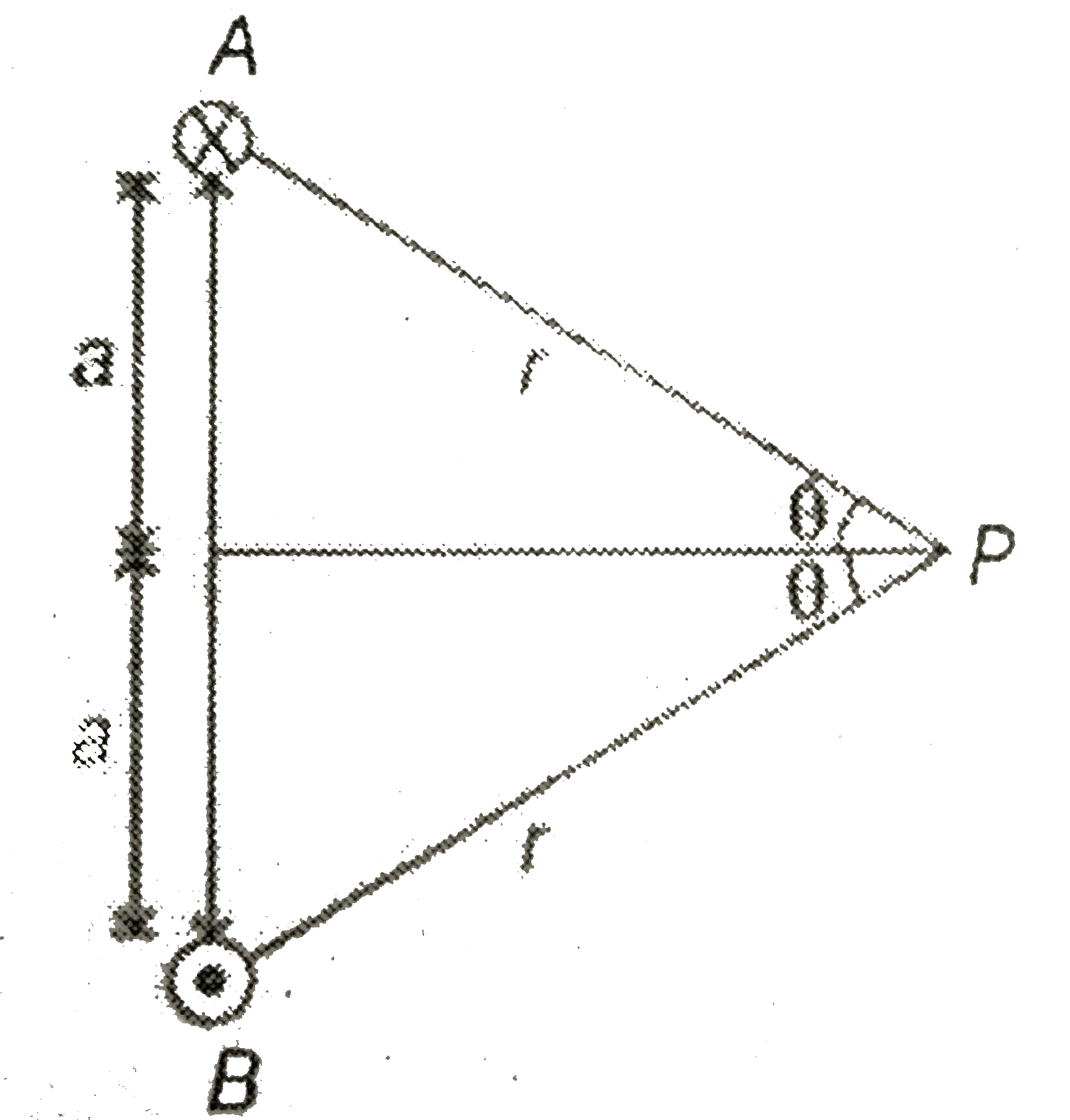
View SolutionTwo long parallel wire A and B situated perpendicuilar to the plane of the paper at a distance 2a are carrying equal currents I in opposite direction as show in the figure . The value of magnetic induction at point P situated at equal distance r from both the wires will be
View SolutionTwo parallel straight long conducting wires, which are placed at a distance r from each other, are carrying equal currents I in opposite directions. The value of magnetic induction at a point situated at a point situated x from one wire in between the wires will be:
View SolutionTwo thin, long, parallel wires, separated by a distance 'd' carry a current of 'i' A in the same direction. They will
View Solution

