Find the resultant magnetic force and torque on the loop.
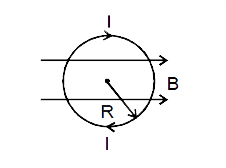
F−→res=0,(∴ loop)
and →τ=iπR2B(−ˆj)
using the above method
Topper's Solved these Questions
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-1
50 Videos
- MAGNETISM BOOK - MOTIONCHAPTER - MAGNETISM EXERCISE - EXERCISE-2 (Level-I)
40 Videos
- LOGIC GATESBOOK - MOTIONCHAPTER - LOGIC GATESEXERCISE - EXERCISE - 2
10 Videos
- MAGNETISM -1BOOK - MOTIONCHAPTER - MAGNETISM -1EXERCISE - Exercise - 3 SECTION -A
56 Videos
Similar Questions
Knowledge Check
Assertion: A closed current carrying loop behaves like a magnetic dipole.
Reason: Force and torque on the loop is zero as shown in figure.
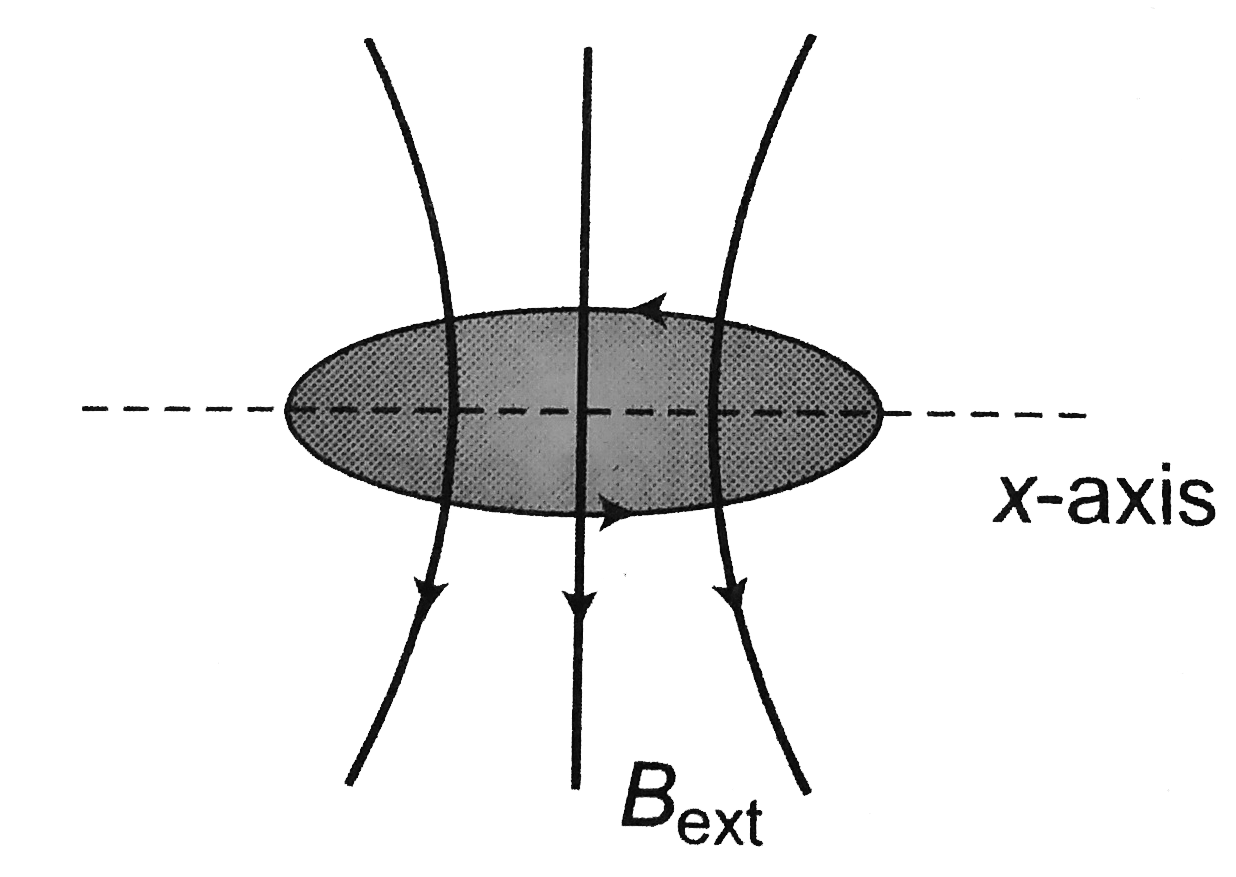 AIf both the assertion and reason are true and reason is a true explantion of the assertion.BIf both the assertion and reason are true but the reason is not true the correct explantion of the assertion.CIf the assertion is true but reason falseDIf both the assertion and reason are false.
AIf both the assertion and reason are true and reason is a true explantion of the assertion.BIf both the assertion and reason are true but the reason is not true the correct explantion of the assertion.CIf the assertion is true but reason falseDIf both the assertion and reason are false.
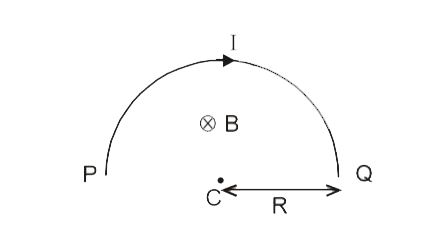
In the figure shown find the resultant magnetic force and torque about ‘C’, and ‘P’.
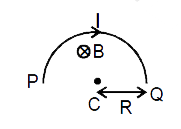
View SolutionIn the figure shown find the resultant magnetic force and torque about 'C' and 'P'.
View Solution(a) Derive the expression for the magnetic energy stored in an inductor when a current I develops in it. Hence, obtain the expression for the magnetic energy density.
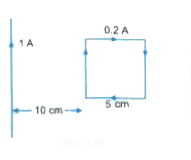
(b) A square loop of sides 5 cm carrying a current of 0.2 A in the clockwise direction is placed at a distance of 10 cm from an infinitely long wire carrying a current of 1 A as shown in Fig. 6.66. Calculate (i) the resultant magnetic force, and (ii) the torque, if any, acting on the loop.
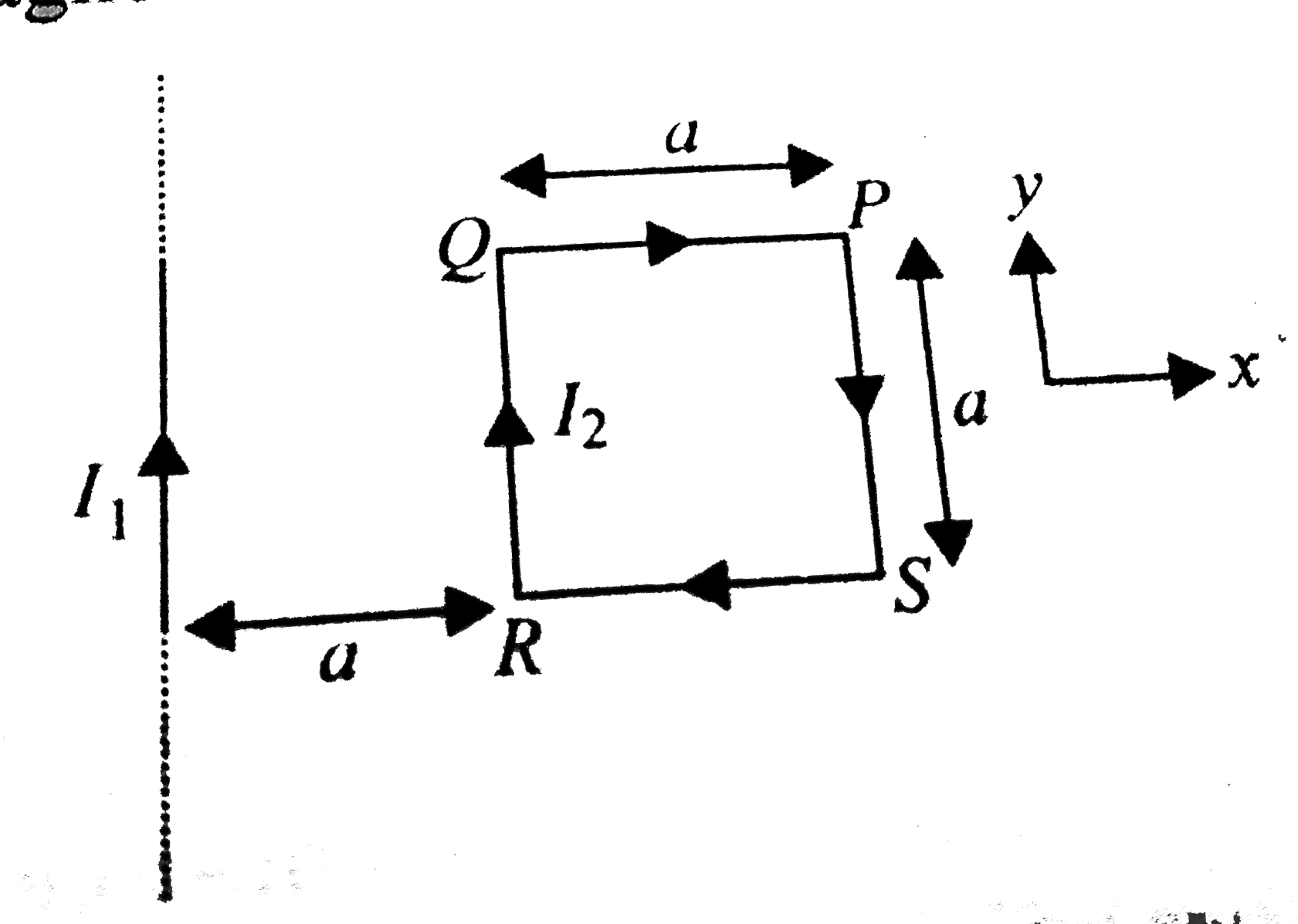
View SolutionFind the magnetic force on loop PQRS due to the wire.
View SolutionIf several forces act on a particle, the total torque on the particle mauy be obtained by first finding the resultant force and then taking torque of this resultant. Prove this. Is this result valid for the forces actin on difeent partivles of a body in such a way that their lines of acting intersect at a common point?
View SolutionA current loop of arbitrary shape lien in a uniform magnetic field B. show that the net magnetic force acting on the loop is zero.
View SolutionTwo similar current loops are placed with their planes mutually perpendicular and centres of both loop lie on the origin. Find the ratio of resultant magnetic field at common centre to the individual magnetic field at common centre.
View Solution


