A box of $1.00 m^{3}$ is filled with nitrogen at $1.50$ atm at 300 k. The box has a hole of an area 0.010 $m m^{2} .$ How much time is required for the pressure to reduce by 0.10 atm, if the pressure outside is 1 atm.

Video Solution

Text Solution

Verified by Experts

Given volume of the box $V = 1 .00 m^{3}$
Area $= a = 0.0010 m m^{2}$
$= 8.01 \times 10^{- 6} m^{2}$
$= 10^{- 8} m^{2}$

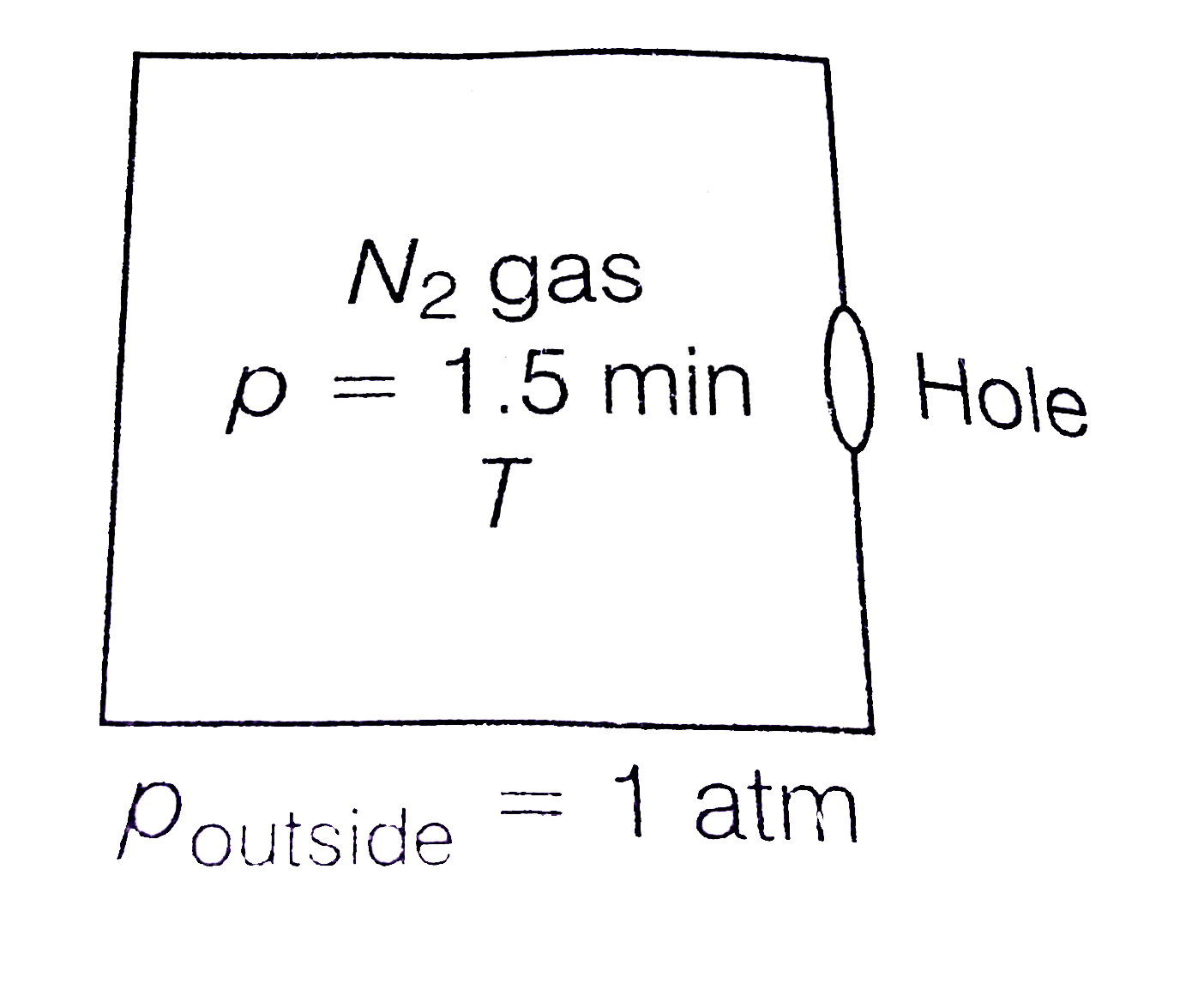
Temperature outside = Temperature inside
initial pressure inside the box =1.50 atm.
Final pressure inside the box =0.10 atm. Assuming
$V_{i x} =$ Speed of nitrogen molecule inside the box along x- direction $n_{i}$ = Number of molecules per unit volume in a time interval of of $Δ T .$ all the particles at a distance $(V_{i x} Δ T)$ will collide the hole and the wall the particle colliding along the hole will escape out reducing the pressure in the box.
Let area of the wall number of particles colliding in time
$Δ t = \frac{1}{2} n_{i} (V_{i x} Δ t) A$
$\frac{1}{2}$ is the factor because all the particles along x- direction are behaving randomly . Hence half of these are colliding against the walls on either side.
$Inside the box V_{i x}^{2} + V_{i x}^{2} + V_{i z}^{2} = V_{rms}^{2}$
$∴ V_{i x}^{2} = \frac{V_{rms}^{2}}{3} (V_{i x} = V_{i y} = V_{i z})$
$or \frac{1}{2} m v_{rms}^{2} = \frac{3}{2} k_{B} T ⎡ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ V_{rms} = Root mean squre velocity K_{B} = Boltzmann constant T = Temperature$
$\Rightarrow V_{rms}^{2} \frac{3 k_{B} T}{m}$
$\Rightarrow V_{rms} = \sqrt{\frac{3 K_{B} T}{m}}$
[According to kinetic theory of gases]
$Nos v_{i x}^{2} = \frac{V_{rms}^{2}}{3} = \frac{1}{3} \times \frac{3 K_{B} T}{m}$
$or v_{i x}^{2} = \frac{K_{B} T}{m}$
$∴$ Number of particles colliding in time
$Δ t = \frac{1}{2} n_{i} \sqrt{\frac{K_{B} T}{m}} Δ t A$
If particles collide along hole, they move out. Simailrly, outer particles colliding along hole will move in.
If a = area of hole
Then , net particle flow in time $Δ t = \frac{1}{2} (n_{1} - n_{2}) \sqrt{\frac{k_{B} T}{m}} Δ t A$
[Temperature inside and outside the box are equal]
$p V = μ R T \Rightarrow \frac{p V}{R T}$
Let n=number density of nitrogen $= \frac{ν N_{A}}{V} = \frac{p N_{A}}{R T} [∴ \frac{μ}{V} = \frac{p}{R T}]$
Let $N_{A} =$ Avogardro's number
If after time $τ$ pressure inside changes from p to $p_{1}^{1}$
$∴ n_{1} = \frac{v N_{A}}{R T}$
Now number of molecules gone out $= n_{1} V - n_{1} V$
$= \frac{1}{2} (n_{1} - n_{2}) \sqrt{\frac{k_{B} T}{m}} τ a$
$∴ \frac{p_{1} N_{A}}{R T} V - \frac{v N_{A}}{R T} V = \frac{1}{2} (P_{1} - P_{2}) \frac{N_{A}}{R T} \sqrt{\frac{K_{B} T}{m}} τ a$
$or \frac{p_{1} N_{A}}{R T} V - \frac{v N_{A}}{R T} V = \frac{1}{2} (p_{1} - p_{2}) \frac{N_{A}}{R T} \sqrt{\frac{k_{B} T}{m}} τ a$
$∴ τ = 2 (\frac{p_{1} - p v_{1}}{p_{1} - p_{2}}) \frac{v}{a} \sqrt{\frac{m}{k_{B} T}}$
Putting hte values from the data given,
$τ = 2 (\frac{1.5 - 1.4}{1.5 - 1.0}) \frac{1 \times 1.00}{0.01 \times 10^{- 6}} \sqrt{\frac{46.7 \times 10^{- 27}}{1.38 \times 10^{- 23} \times 300}}$
$= (\frac{0.1}{0.5}) \frac{1}{10^{- 8}} \sqrt{\frac{4.7}{1.38 \times 3}} \times 10^{- 6}$
$= 2 (\frac{1}{5}) 1 \times 10^{8} \times 10^{- 3} \times \sqrt{\frac{46.6}{4.14}} = \frac{2}{5} \times 10^{5} \sqrt{\frac{45.7}{4.14}}$
$= \frac{2}{5} \times 10^{5} \sqrt{11.28}$
$= \frac{2}{5} \times 3.358 \times 10^{5} = \frac{6.717}{5} \times 10^{5} = 1.343 \times 10^{5} s$

Updated on:21/07/2023

A weather balloon filled with hydrogen at 1 atm and 300K has volume equal to 12000 litres. On ascending it reaches a place where temperature is 250K and pressure is 0.5atm. The volume of the balloon is:
A24000 litres
B20000 litres
C10000 litres
D12000 litres
10 moles of an ideal gas are compressed isothermally and reversibly at 200°C from a pressure of 1 atm to a pressure of S atm. Then
A $Δ U = 0, Δ H = 0$
B $Δ U \neq 0, Δ H = 0$
C $Δ U = 0, Δ H \neq 0$
D $Δ U \neq 0, Δ H \neq 0$
A weather balloon filled with hydrogen at $1$ atm and $300$ K has volume equal to $12000$ liters. On ascending it reaches a place where temperature is $250$ K and pressure is $0.5$ atm. The volume of the balloon is :
A $24000$ liters
B $20000$ liters
C $10000$ liters
D $12000$ liters