The mixture of a pure liquid and a solution in a along vertical column (i.e., horizontal dimensions << vertical dimensions) produces diffusion of solute particles and hence a refractive index gradient along the vertical dimension. A ray of light entering the column at right angles to the vertical is deviated from its original path. Find the deviation in travelling a horizontal distance d<<h, the height of the column.
Video Solution
Text Solution
Let us consider a portionh of a ray betweehn x and x+dx inside the liquid . Let the angle of incidence at x be θ and let it enter it thin column at height y. Because of the bending it shall emerge at x+dx with and angle θ+dthη and at a height y+ dy. From Snell's law

μ(y)sinθ=y(y+dy)sin(θ+dθ)
or μ(y)sinθ,(μ(y)+dμdydy)(sinθcosdθ+cosθsindθ)
or μ(y)sinθμ(y)cosθdθ+dμdydysinθ
or μ(y)cosθdθ,dμdydysinθ
dθ,−dμμdydytanθ
But tanθ=dxdy (from the figure)
On solving , we have
∴ dθ=−1dμμdydx
Solving this variable separable form of differential equation.
∴ θ=−1dμμdy∫dodx=−1dμμdyd
|
Topper's Solved these Questions
- NUCLEIBOOK - NCERT EXEMPLARCHAPTER - NUCLEIEXERCISE - Nuclei
40 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITBOOK - NCERT EXEMPLARCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIAL,DEVICES AND SIMPLE CIRCUITEXERCISE - Semiconductor Electronics: Material,Devices And Simple Circuit
26 Videos
Similar Questions
Knowledge Check
A prism having an apex angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown in figure. Through what total angle is the ray is deviated after reflection from the mirror ?
 A176∘B4∘C178∘D2∘
A176∘B4∘C178∘D2∘A prism having an apex angle 4o and refraction index 1.5 is located in front of a vertical plane mirror as shown in figure. Through what total angle is the ray deviated after reflection from the mirror
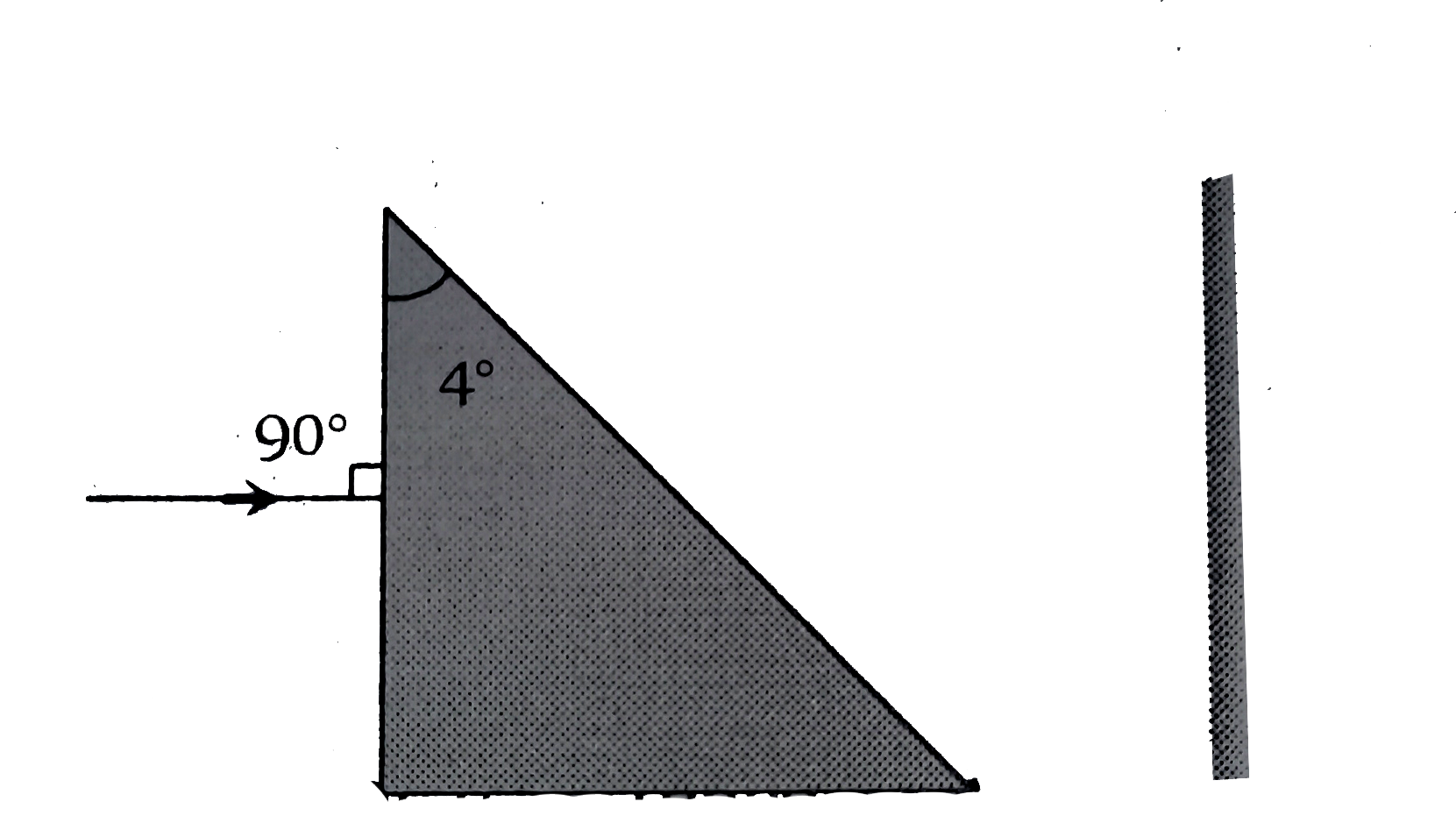 A176∘B4∘C178∘D2∘
A176∘B4∘C178∘D2∘The angle of a prism is 60∘ and its refractive index is √2 . The angle of minimum deviation suffered by a ray of light in passing through it is
AAbout 20∘B30∘C60∘D45∘
What are horizontal rows and vertical columns of the periodic table called ?
View SolutionA force of 4N is inclined at an angle of 60∘ from the vertical. Find out its components along horizontal and vertical directions.

View SolutionA prism having a refracting angle 4∘ and refractive index 1.5 is located in front of a vertical plane mirror as shown. A horizontal ray of light is incident on the prism. What is the angle of incidence at the mirror ?
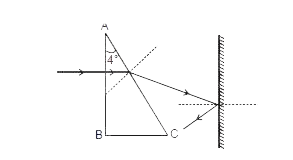
View SolutionA ray of light suffers a minimum deviation when incident on equilateral prism of refractive index √2 The angle of deviation is
View SolutionIf the angle (θ) between velocity vector and the acceleration vector of a moving particle is 90∘<θ<180∘, then the path of the particle is
View Solution
