A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0

(i) consider the figure given below

During the propagation of electromagnetic wave a along z-axis let electric field vector (E) be along x-axis and megnetic field vector B along y-axis i.e., E=E0ˆi and B=B0ˆj
Line intergral of E over the closed rectangular path 1234 in x-z plane of the figure
∮E.dl=2∫1E.dl+3∫2E.dl+4∫3E.dl+1∫4E.dl
=2∫1E.dlcos90+3∫2E.dlcos0+4∫3E.dlcos90+1∫4E.dlcos180∘
=E0h[sin(kz2−ωt)−sin(kz1−gωt)]
(ii) For evaluating ∫B.ds, let us consider the rectangle 1234 to be made of strips of are ds = hdz each.
∫B.ds=∫B.dscos0=∫B.ds=z2∫z1B0sin(kz−ωt)hdz
=−B0hk[cos(kz2−ωt)−cos(kz1−ωt)]

(iii) Given ∮E.dl=0dϕBdt=−ddt∮B.ds
Putting the values from Eqs. (i) and (ii) we get
E0h[sin(kz2−ωt)−sin(kz1−ωt)]
=−ddt[Byhk{cos(kz2−ωt)−cos(kz1−ωt)]
=Byhkω[sin(kz2−ωt)−sin(kz1−ωt)]
⇒ E0=B0ωK=Byc
⇒ E0B0=c
(iv) For evaluating ∮B.dl let us consider a loop 1234 in y-z plane as shown in figure given below
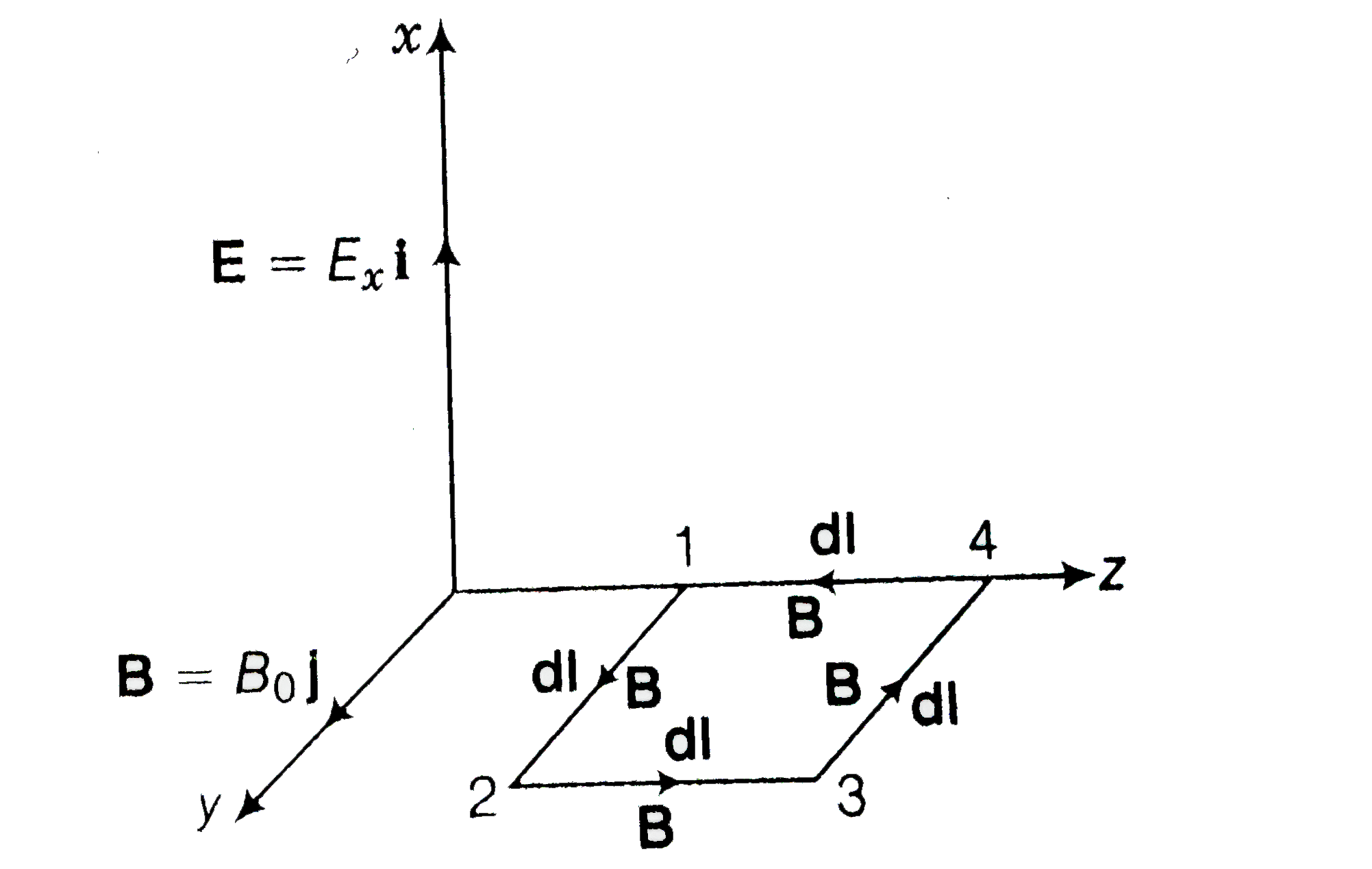
∮B.dl=2∫1B.dl+3∫2B.dl+4∫3B.dl+1∫4B.dl
=2∫1B.dlcos0+3∫2B.dlcos90∘+4∫3B.dlcos180∘+1∫4B.dlcos90∘
=B0h[sin(kz1−ωt)−sin(kz2−ωt)
Now to evaluate ϕE=∫E.ds let us consider the rectangle 1234 to be made of strips of area hd2 each.

ϕE∫E.ds=∫Edscos0=∫Eds=z2∫z1E0sin(kz1−ωt)hdz
=−E0hK[cos(kz2−ωt)−cos(kz1−ωt)]
∴dϕEdt=E0hωK[sin(kz1−ωt)−sin(kz2−ωt)]
∮B.dl=μ0(l+ε0ϕEdt)I=conduction current
∴∮B.dl=μ0εdϕEdt
Using relations obtained in Eqs. (iii) and (iv) and simplifying we get
B0=E0ωμ0ε0K
⇒ E0B0ωK=1μ0ε0
But E0B0=c and ω=ck
⇒ c.c=1μ0ε0thereforec=1√μ0ε0
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTION Book:NCERT EXEMPLARChapter:ELECTROMAGNETIC INDUCTION Exercise:Electromagnetic Induction
Explore 32 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCEBook:NCERT EXEMPLARChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCEExercise:Electrostatic Potential And Capacitance
Explore 33 Videos
Similar Questions
A plane EM wave travelling in vacuum along z-direction is given by E=E0 sin (kz−ωt)ˆi and B=B0 sin (kz−ωt)ˆj
(i) Evaluate ∫E.dl over the rectangular loop 1234 shown in figure.
(ii) Evaluate ∫B.ds over the surface bounded by loop 1234.
(iii) Use equation ∫E.dl=−dϕBdt to prove E0B0=c.
(iv) By using similar proces and the equation
∫B.dl=μ0I+ε0dϕEdt, prove that c1√μ0ε0

View SolutionA plane EM wave travelling along z-direction is described by E=E0sin(kz−ωt)ˆi and B=B0sin(kz−ωt)ˆjThe time averaged intensity of the wave is given by I(av)=(18cɛ0E20)α. Find α
View Solution
Knowledge Check
A electromagnetic wave going through a medium is given by E=E0sin(kx–ωt)andB=B0sin(kx–ωt) then
AE0k=B0ωBIf Electric is in Z direction them magnetic field should be in -y direction.CBoth ‘A’ and ‘B’ are correctDOnly A is correctDimensions of ε0dϕEdt are same as that of
A[AT]B[A]C[ML2T−2]D[ML−1T−2]The maxwell’s equation :
∮→B.→dl=μ0(i+ɛ0.dϕEdt) is a statement of -AFaraday’s law of inductionBModified Ampere’s lawCGauss’s law of electricityDGauss’s law of magnetism
A plane EM wave travelling along z direction is described by
E=E0sin(kz−ωt)ˆiandB=B0sin(kz−ωt)ˆj.
show that
(i) The average energy density of the wave is given by uav=14ε0E20+14B20μ0.
(ii) The time averaged intensity of the wave is given by Iav=12cε0E20.
View SolutionDimensions of ε0dϕEdt are same as that of
View SolutionAn electromagnetic wave travelling along z-axis is given as E=E0 cos (kz−ωt). Choose the correct options from the following
View SolutionAn electromagnetic wave is propagating in vacuum along z-axis, the electric field component is given by Ex=E0sin(kz−ωt). Then magnetic components is
View SolutionAn electromagnetic wave is propagating in vacuum along z-axis, the electric field component is given by Ex=E0sin(kz−ωt), then magnetic component is
View Solution

