Polynting vectors →S is defined as a vector whose magnitude is equal to the wave intensity and whose direction is along the direction of wave propogation. Mathematically, it is given by →S=1μ0→E×→B. Show the nature of S vs t graph
Video Solution
Text Solution
Consider and electromagnetic waves. Let E varying along y-axis B is along z-axis and propagation of wave be along x-axis . Then E×B will tell the direction of propagation of energy flow in electomegnetic wave along x-axis.
E=E0 sin(ωt−kx)hagj
B=B0 sin (ωt−kx)ˆk
S=1μ0(E×B)=1μ0E0B0 sin2(ωt−kx)[ˆj׈k]
E0B0μ0sin2(ωt−kx)ˆi
The variation of |S| with time t will be as given in the figure below
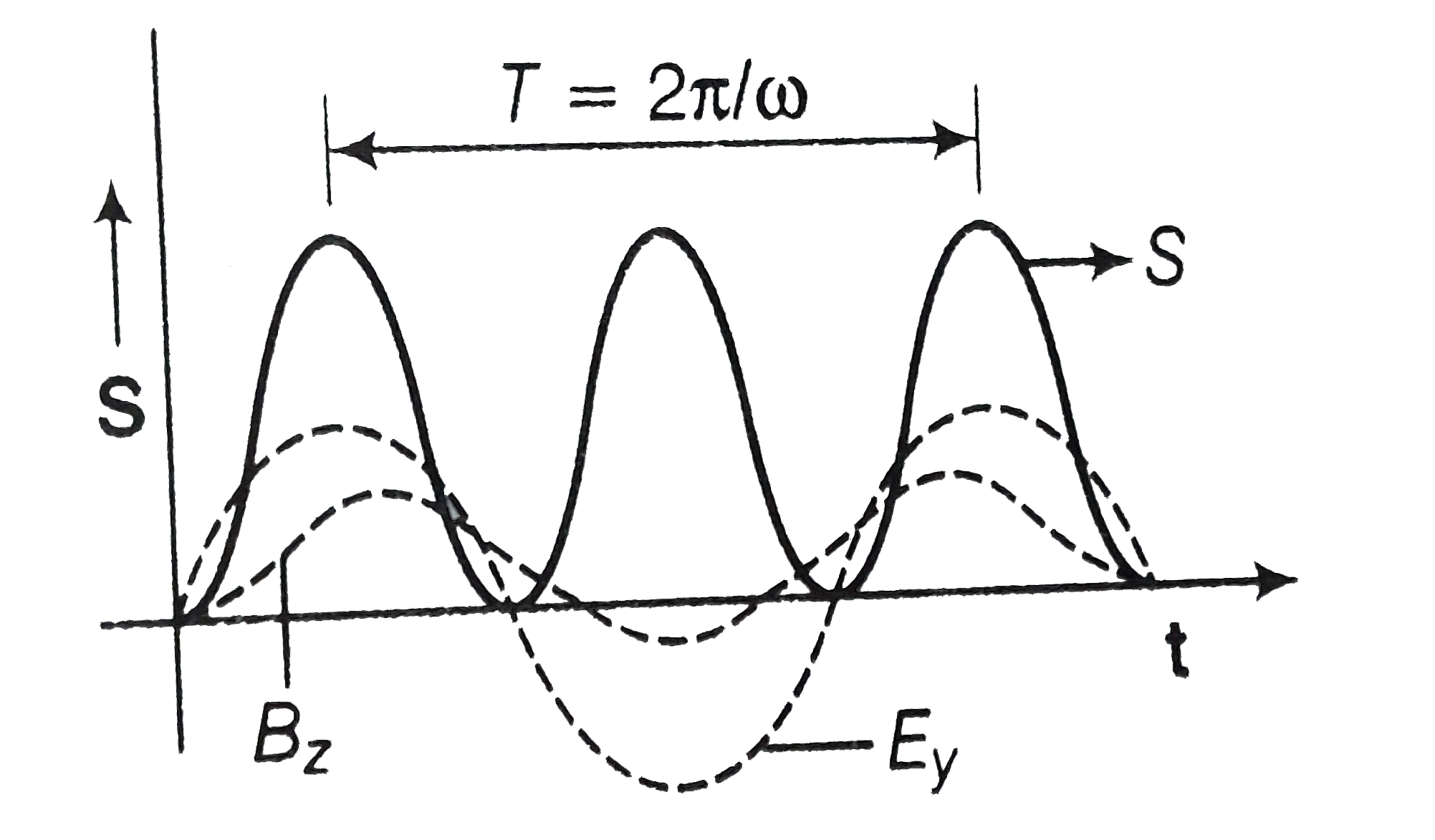
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Poynting vectors →S is defined as →S=1μ0→E×→B. The average value of '→S' over a single period 'T' is given by
AE20/2cμ0BE20/cμ0C2E022/cμ0DE20/cμ20If →E and →B represent electric and magnetic field vectors of the electromagnetic wave, the direction of propagation of electromagnetic wave is along
A→B→BC→B×→ED→E×→BA transverse wave, whose amplitude is 0.5 m wavelength is 1 m and frequency is 2Hz. is travelling along positive x direction. The equation of this wave will be-
Ay=0.5cos(2πx−4πt)By=0.5cos(2πx−4πt)Cy=0.5sin(πx−2πt)Dy=0.5cos(2πx−2πt)
Prove that the normal to the plane containing three points whose position vectors are →a,→b,→c lies in the direction →b×→c+→c×→a+→a×→b.
View SolutionIn an electromagnetic wave the electric field vector and magnetic field vector are given as →E=E0ˆi and →B=B0ˆk respectively. The direction of propagation of electromagnetic wave is along:
View SolutionThe position vectors of two given points PandQ are 8ˆi+3ˆjand2ˆi−5ˆj respectively; find the magnitude and direction of the vector (→PQ)
View SolutionYou are given a vector,
→P=1√2cosθˆi+1√2sinθˆj What is the unit vector in the direction of →P ?
View SolutionA vector →A When added to the vector →B=3ˆi+4ˆj yields a resultant vector that is in the positive y-direction and has a magnitude equal to that of →B. Find the magnitude of →A.
View Solution