A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.
(i) Given , the induced electric field at a distance r from the wire inside the cable is
E(s,t)=μ0I0vcos(2πvt)In(sa)ˆk
Now displacement current density ,
J0=ε0dEdt=ε0ddt[μ0I0vcos(2πvt)In(sa)ˆk]
=ε0μ0I0vddt[cos2πvt]In(sa)ˆk
=1c2I0v2π[−sin2πvt]In(sa)ˆk
=V2C22πI0sin2πvtIn(as)ˆk [∴l4sa=−l4as]
=1λ22πI0In(as)sin2πvtˆk
=2πI0λ2Inassin2πvtˆk
(ii) Id=∫Jdsdsd0=a∫s=0Jdsds2π∫0d0=a∫s=0Jdsds×2π
=(2πλ)2
⇒ =(2πλ)2I0a∫s=0In(as)12d(s2).sin2πvt
=a22(2πλ)2I0sin2πvta∫s=0In(as).d(sa)2
=a24(2πλ)2I0sin2πvta∫s=0In(as)2.d(sa)2
=−a24(2πλ)2I0sin2πvta∫s=0In(sa)2.d(sa)2
=−a24(2πλ)2I0sin2πvt×(−1) ⎡⎢⎣∴a∫s=0In(sa)2d(sa)2=−1⎤⎥⎦
∴Ida24(2πλ)2I0sin2πvt
⇒ =(2πa2λ)2I0sin2πvt
(iii) the displacement current
I0=(2πa2λ)2I0sin2πvt=I0dsin2πvt
Here I0d=(2πa2λ)2I0=(aπλ)2I0
I0dI0=(aπλ)2
Topper's Solved these Questions
Similar Questions
A long straight cable of length l is placed symmetrically along z-axis and has radius a(<<l). The cable consists of a thin wire and a co- axial conducting tube. An alternating current I(t)=I0 sin (2πvt). Flows down the central thin wire and returns along the co-axial conducting tube. the induced electric at a distance s from the wire inside the cable is
E(s,t)=μ0I0v cos (2πvt)In(sa)ˆk.
(i) Calculate the displacement current density inside the cable.
(ii) Integrate the displacement current density across the cross- section of the cable to find the total displacement current Id.
(iii) compare the conduction current I0 with the displacement current Id0.View SolutionWhat is the electric potential of the neutral wire in a main supply cable
View Solution
Knowledge Check
- Question 1 - Select One
A long straight cable contains 7 strands of wire each carrying a current of 5 A. The magnetic induction at a distance of 2 cm from the axis of the cable is
A5×10−5 TB3.5×10−4 TC3.5×10−4 TD1.1×10−3 T - Question 2 - Select One
A current i ampere flows along the inner conductor of a coaxial cable and returns along the outer conductor of the cable, then the magnetic induction at any point outside the conductor at a distance r meter from the axis is
A∞BZeroCμ04π2irDμ04π2πrr - Question 3 - Select One
Current flows through a straight, thin-walled tube of radius r. The magnetic field at a distance x from the axis of the tube has magnitude B.
AB∝x, for 0 lt x lt rBB∝1/x , for 0 lt x lt rCB=0 , for 0≤x<rDB=0 , only for x=0
List the colours of the three wires in the cable connected to the plug of an electric iron.
View SolutionA wire carries an alternating current i=i0 sin omega t. In there an electric field in the vicinity of the wire?
View SolutionA coaxial cable consists of a thin inner current carrying conductor fixed along the axis of a hollow current conductor, Let B1 and B2 be the magnetic fields in the region between the conductors, and outside the conductor respectively.
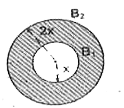 View Solution
View SolutionWhen there is an electric current through a conducting wire along its length, then an electric field must exist
View SolutionA solenoid of radius R number of turn per unit length n and length L has a current I=I0cosωt. The value of induced electric field at a distance of r outside the solenoid, is :
View Solution

