A particle of mass 1 kg is moving along x - axis and a force F is also acting along x -axis in such a way that its displacement is varying as : . Find work done by force F when it will move 2m.
12 J
16 J
32 J
42 J
The correct Answer is:A
To solve the problem step by step, we will follow the principles of kinematics and dynamics to find the work done by the force F.
Step 1: Understand the displacement function
The displacement of the particle is given by the equation:
x=3t2
This indicates how the position of the particle changes with time t.
Step 2: Find the velocity
To find the velocity v, we differentiate the displacement x with respect to time t:
v=dxdt=d(3t2)dt=6t
Step 3: Find the acceleration
Next, we differentiate the velocity v to find the acceleration a:
a=dvdt=d(6t)dt=6m/s2
This indicates that the acceleration is constant.
Step 4: Calculate the force using Newton's second law
Using Newton's second law, the force F acting on the particle can be calculated as:
F=m⋅a
Given that the mass m=1kg:
F=1⋅6=6N
Step 5: Determine the work done by the force
The work done W by the force when the particle moves a displacement s=2m is given by the formula:
W=F⋅s
Since both the force and displacement are in the same direction (along the x-axis), we can directly multiply:
W=6N⋅2m=12J
Conclusion
The work done by the force F when the particle moves 2 meters is:
12J
The displacement of the particle is given by the equation:
x=3t2
This indicates how the position of the particle changes with time t.
To find the velocity v, we differentiate the displacement x with respect to time t:
v=dxdt=d(3t2)dt=6t
Next, we differentiate the velocity v to find the acceleration a:
a=dvdt=d(6t)dt=6m/s2
This indicates that the acceleration is constant.
Using Newton's second law, the force F acting on the particle can be calculated as:
F=m⋅a
Given that the mass m=1kg:
F=1⋅6=6N
The work done W by the force when the particle moves a displacement s=2m is given by the formula:
W=F⋅s
Since both the force and displacement are in the same direction (along the x-axis), we can directly multiply:
W=6N⋅2m=12J
The work done by the force F when the particle moves 2 meters is:
12J
Similar Questions
Force acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
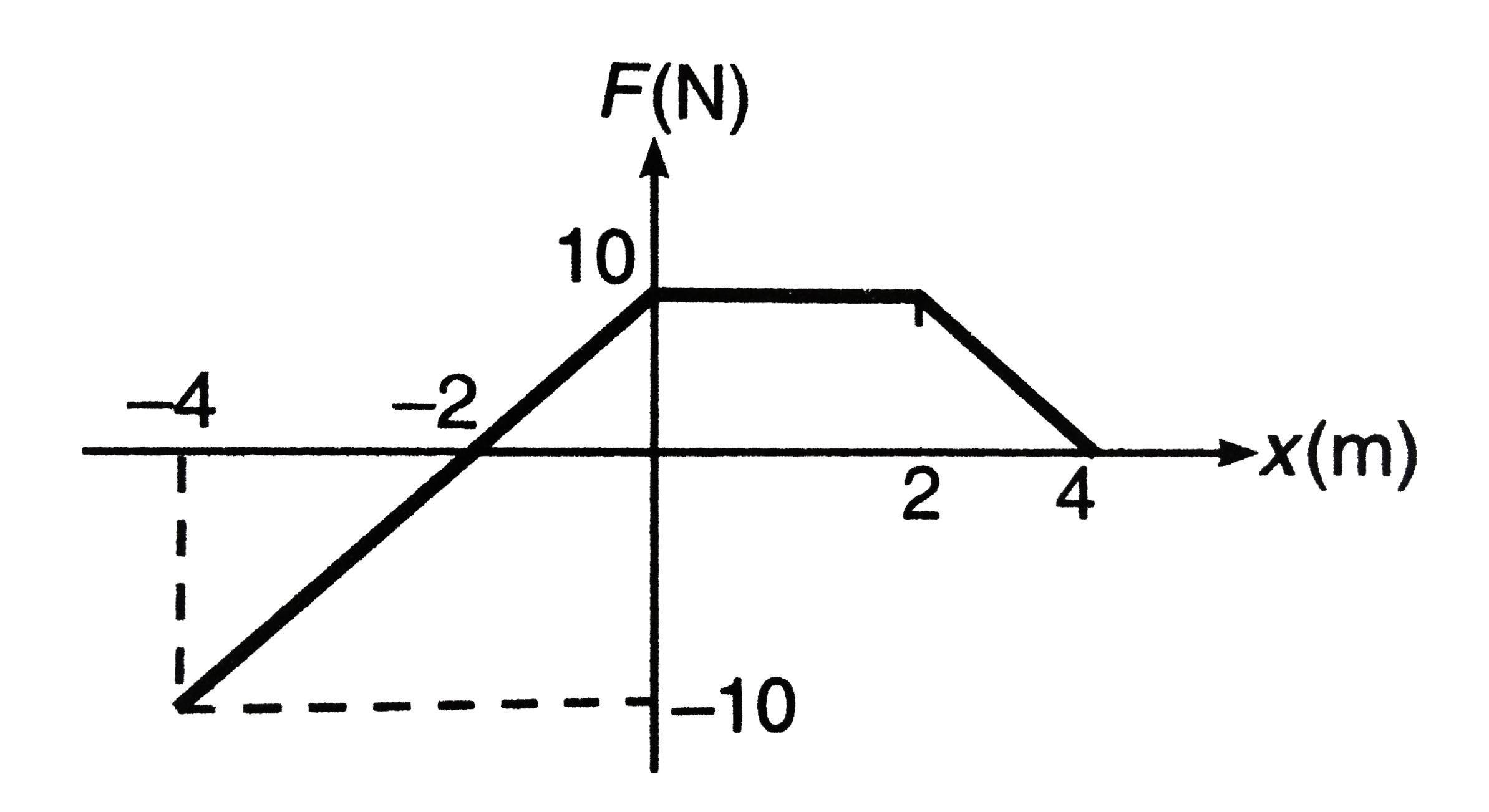 .
.
View SolutionThe position of a particle of mass 10kg moving along x- axis varies with time as x=2+t2(x is in meter and t is in second).Then work done by net force from t=0 to till body attains velocity of 10m/s is ?
View Solution
Knowledge Check
A particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
A144 JB72 JC108 JD216 JA particle is moving along the x-axis and force acting on it is given by F=F0sinωxN, where ω is a constant. The work done by the force from x=0 to x=2 will be
AF0ω(1−cosω)BF02ω(1−cos2ω)C2F0sin2ωωDF0ω(1+cos2ω)A particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
A12kx2B12kv2C12mv2D2mv2
A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
View SolutionThe position (x) of a particle of mass 2 kg moving along x-axis at time t is given by x=(2t3) metre. Find the work done by force acting on it in time interval t=0 to t=2 is :-
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
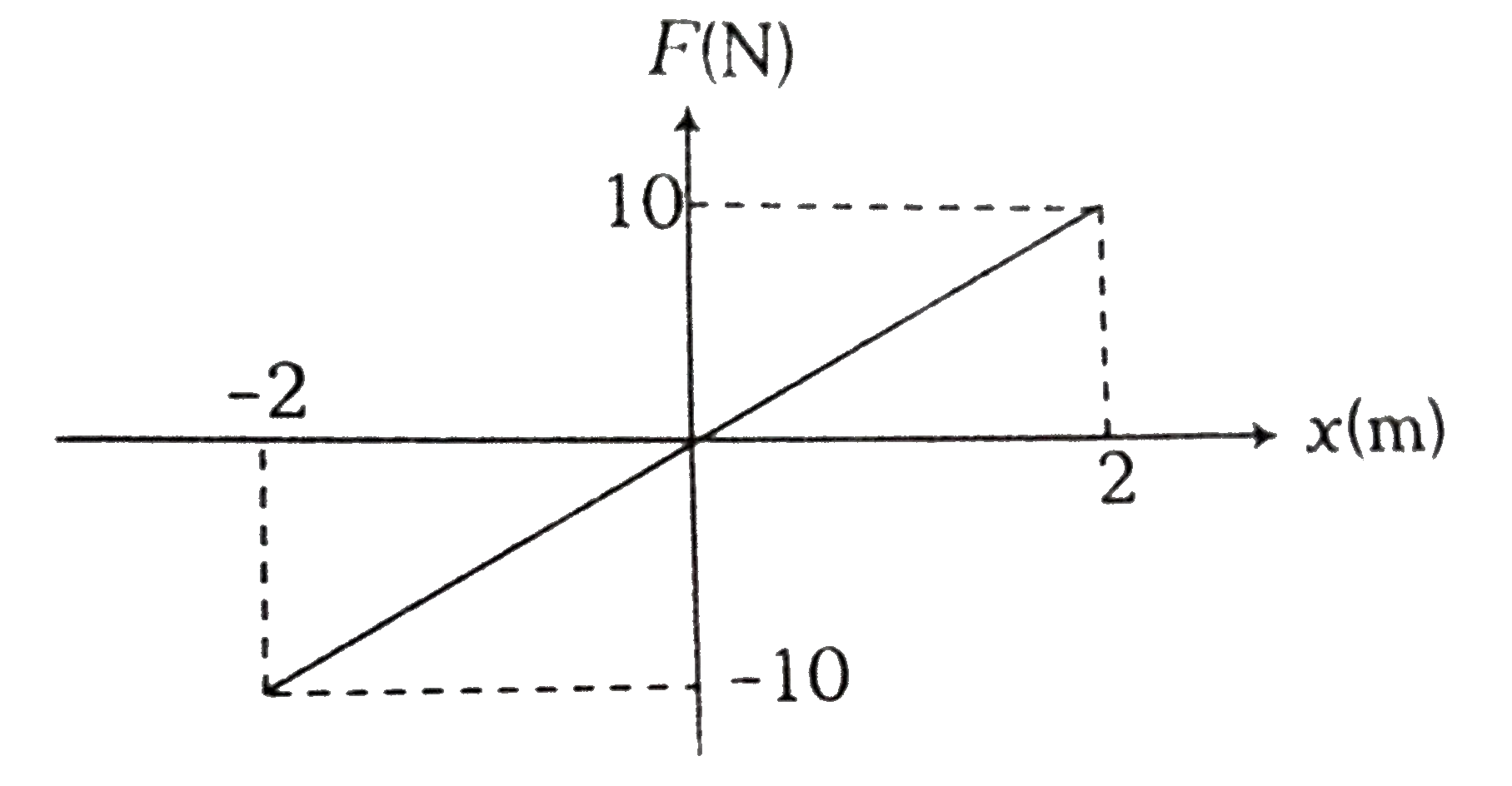
View SolutionA force of (5 +3x) N acting on a body of mass 20 kg along the x-axis displaces it from x= 2 m to x = 6 m . The work done by the force is
View SolutionA force of (5 +3x) N acting on a body of mass 20 kg along the x-axis displaces it from x= 2 m to x = 6 m . The work done by the force is
View Solution
