A force F=−Kx2(x≠0) acts on a particle along the X-axis . Find the work done by the force in displacing the particale from x = +a to x = + 2a. Take K as a positive constant . Solution in Telugu
Force acting on the particle , F=−Kx2
Total amount of work done to displace the particle from x = +a to x = +2a is ,
W=∫dW=∫x=2ax=aFbx
⇒W=∫2ax=a−Kx2dx=−K∫x=2ax=a1x2dx
=−K∫x=2ax=ax−2dx=K[x−1]x=2ax=a
=K[12a−1a]=K[−12a]=−K2a
Topper's Solved these Questions
- WORK , ENERGY AND POWERBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - WORK , ENERGY AND POWEREXERCISE - VERY SHORT ANSWER QUESTIONS
15 Videos
- WORK , ENERGY AND POWERBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - WORK , ENERGY AND POWEREXERCISE - SHORT ANSWER QUESTIONS
7 Videos
- TS MARCH- 2019BOOK - VGS PUBLICATION-BRILLIANTCHAPTER - TS MARCH- 2019EXERCISE - SECTION B
7 Videos
- WORK AND ENERGYBOOK - VGS PUBLICATION-BRILLIANTCHAPTER - WORK AND ENERGYEXERCISE - CONCEPTUAL UNDERSTANDING - AESTHETIC SENSE, VALUES AND DAILY LIFE CONCERN TO BIODIVERSITY
16 Videos
Similar Questions
If a bomb ar rest explodes into two pieces, the pieces must travel in opposite directions . Explain .
View SolutionWhat is potential energy ? Derive an expression for the gravitational potential energy .
View SolutionO' is a point on the ground chosen as origin . A body first suffers a displacement of 10√2 mm North -East, next 10 m Noth and finally 10√2 North-West . How far it is from origin ?
View SolutionHuman beings or machines need ……………. to do work.
View SolutionA force F = -K(y hatI + x hatj) (where K is a posive constant ) acts on a particle moving in the xy plane . Starting form the original , the partical is taken along in the positive x axis to the point (x,0) and then partical to they axis the point (x,0) . The total work done by the force F on the particls is
View SolutionA force F=−kx2(x≠0) acts on a particle in x-direction. Find the work done by this force in displacing the particle from. x=+a to x=2a. Here, k is a positive constant.
View SolutionA force F=-K(yhati+xhatj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a, 0) , and then parallel to the y-axis to the point (a, a) . The total work done by the force F on the particle is
View SolutionA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x =-a to x = +2a . .
View SolutionA force F=−kx3 is acting on a block moving along x-axis. Here, k is a positive constant. Work done by this force is
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from
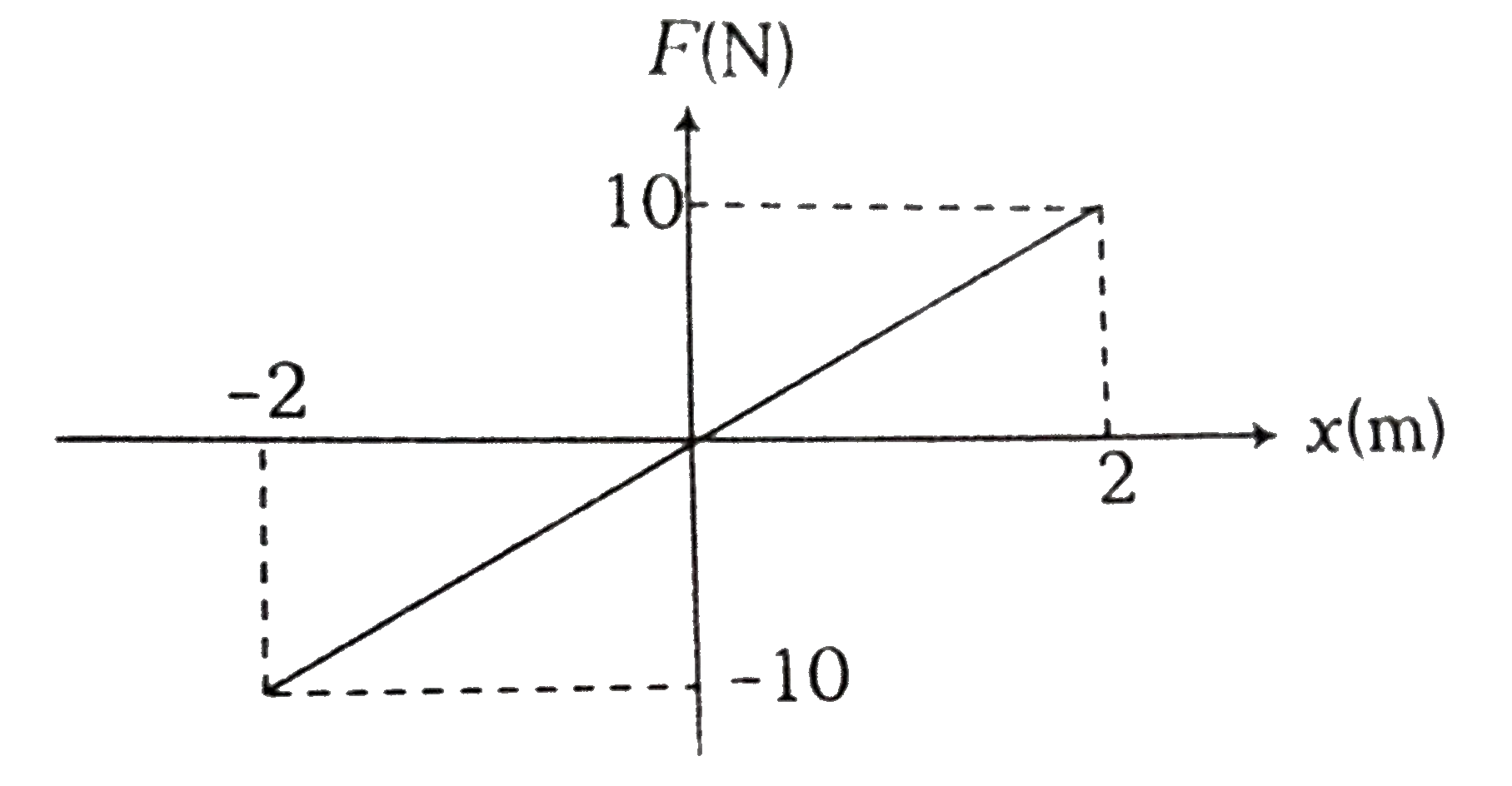
View Solutionबल F=−kx2 द्वारा एक कण को X -अक्ष के अनुदिश x=a से x=2a तक विस्थापित करने में किये गये कार्य कि गणना कीजिये।
View Solutionएक बल F=10+2xएक कण X-अक्ष के अनुदिश कार्यरत है जहाँ F न्यूटन में तथा x मीटर है। बल द्वारा कण को x=0 से x=5 मीटर तक विस्थपित करने में किया गया कार्य ज्ञात कीजिये।
View Solutionबल F=kx2 द्वारा एक कण को x=aसे x=3a तक विस्थपित करने में किये गए कार्य की गणना कीजिये।
View SolutionA force F=−K(yˆi+xˆj) (where K is a positive constant) acts on a particle moving in the x-y plane. Starting from the origin, the particle is taken along the positive x-axis to the point (a,0), and then parallel to the y-axis to the point (a,a). The total work done by the force F on the particle is
View SolutionA variable force F=kx2acts on a particle which is initially at rest. Calculate the work done by the force during the displacement of the particle from x=0mtox=4m. (Assume the constant k=1Nm−2)
View Solution
