A force F is related to the position of a particle by the relation F=(10x2)N . Find the work done by the force when the particle moves from x=2m→x=4m.
W=∫42Fdx=∫4210x2dx=[10x33]42
=103[43−23]=103×56=186.7J
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Long Answer Question
24 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Advanced Problems For Competitions
20 Videos
- WORK, ENERGY AND POWERBOOK - PRADEEPCHAPTER - WORK, ENERGY AND POWEREXERCISE - Very Short Anwer Question.
54 Videos
- THERMODYNAMICSBOOK - PRADEEPCHAPTER - THERMODYNAMICSEXERCISE - Assertion- Reason Type Questions
19 Videos
Similar Questions
Force acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
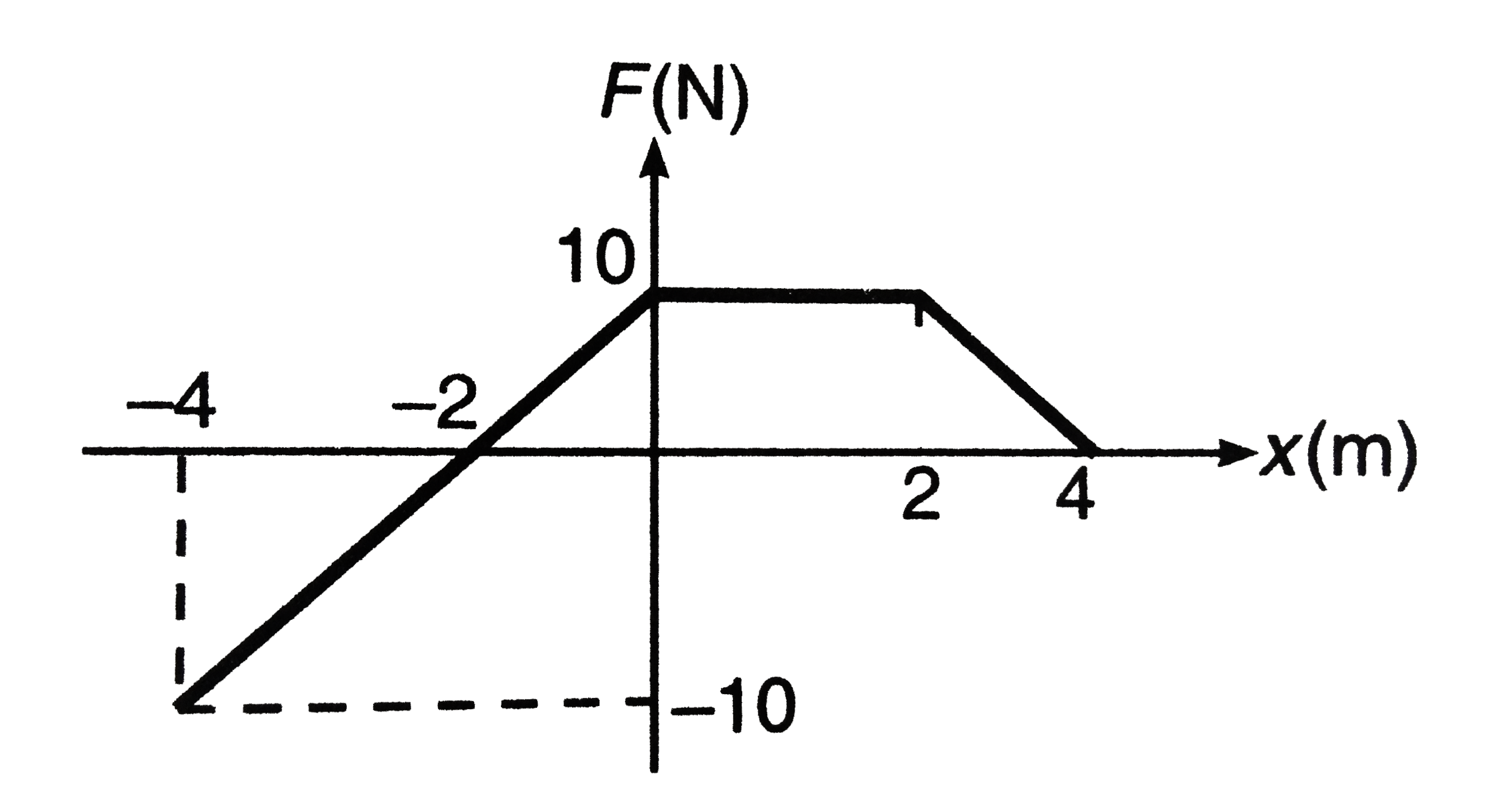 .
.
View SolutionA particle starts from rest from origin and moves along a parabolic path whose equation is y=x2 in the presence of a number of forces.One of the forces acting on the particle is F=(xˆi−4zˆk)N .Find work done by this force F when the particle moves from origin to x=2m.
View Solution
Knowledge Check
A force F is related to the position of a particle by the relation F=(10x2)N. The work done by the force when the particle moves from x= 2 m to x = 4 m is
A563JB560JC5603JD3560JA block is constrained to move along xaxis under a force F=−(2x)N. Find the work done by the force when the block is displaced from x=2m to x=4m
A12JB8JC−12JD−8JA force F acting on a particle varies with the position x as shown in the graph. Find the work done by the force in displacing the particle from x=−a to x=+2a.
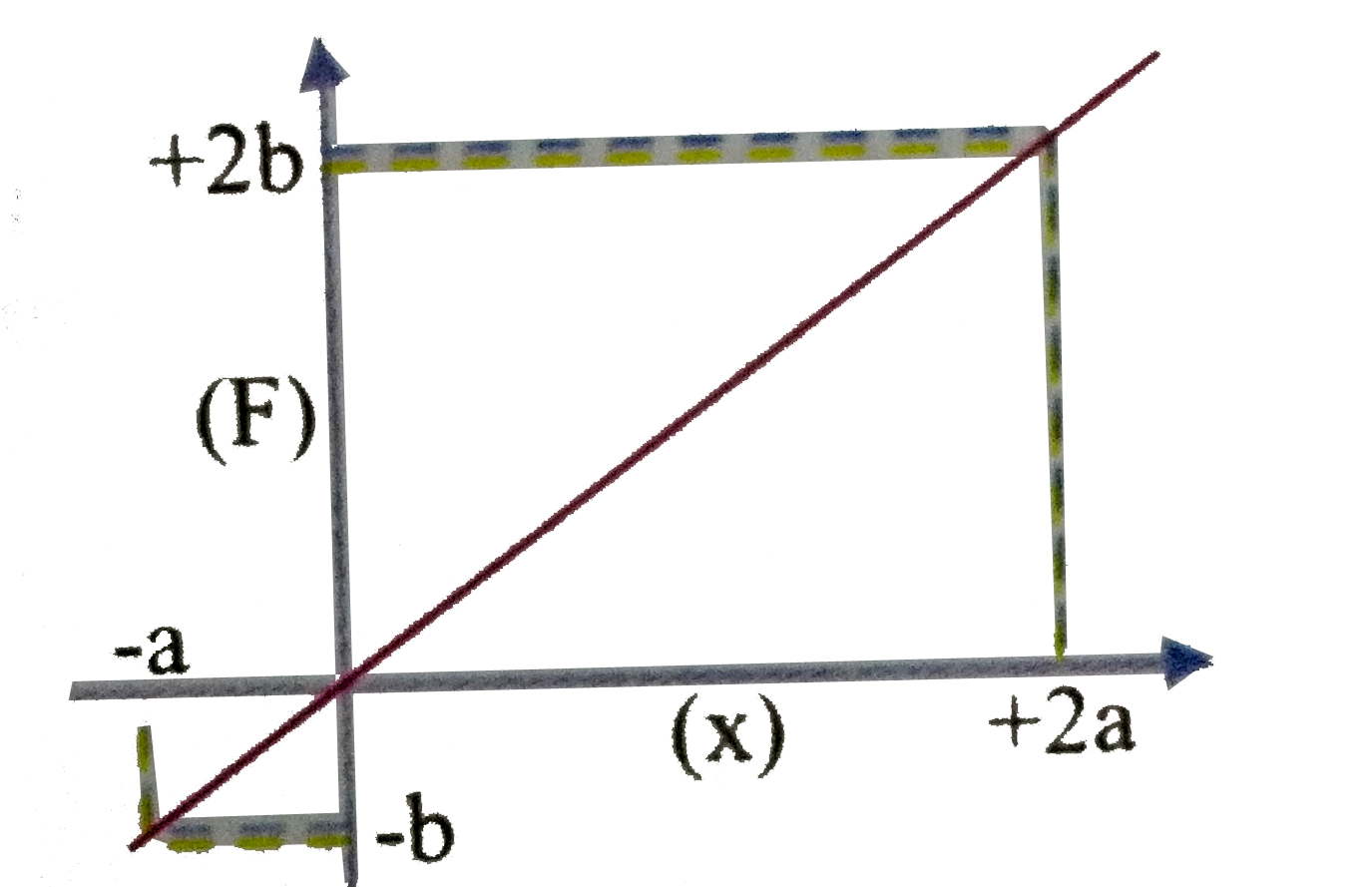 .A3ab2B4ab2C23abD24ab
.A3ab2B4ab2C23abD24ab
Force acting on a particle varies with x as shown in figure. Calculate the work done by the force as the particle moves from x = 0 to x = 6.0 m.
View SolutionThe force on a particle is directed along an x axis and given by F=F0(x/x0−1). Find the work done by the force in moving the particle from x=0 to x=2x0 by (a) plotting F(x) and measuring the work from the graph and (b) integrating F(x).
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA variable force F acts along the x - axis given by F=(3x2)−2x+1N. The work done by the force when a particle of mass 100 g moves from x = 50 cm to x = 100 cm is
View SolutionA particle moves along x -axis under the action of a position dependent force F =(5x2−2x)N. Work done by forces on the particle when it moves from origin to x=3m is
View Solution
