Question

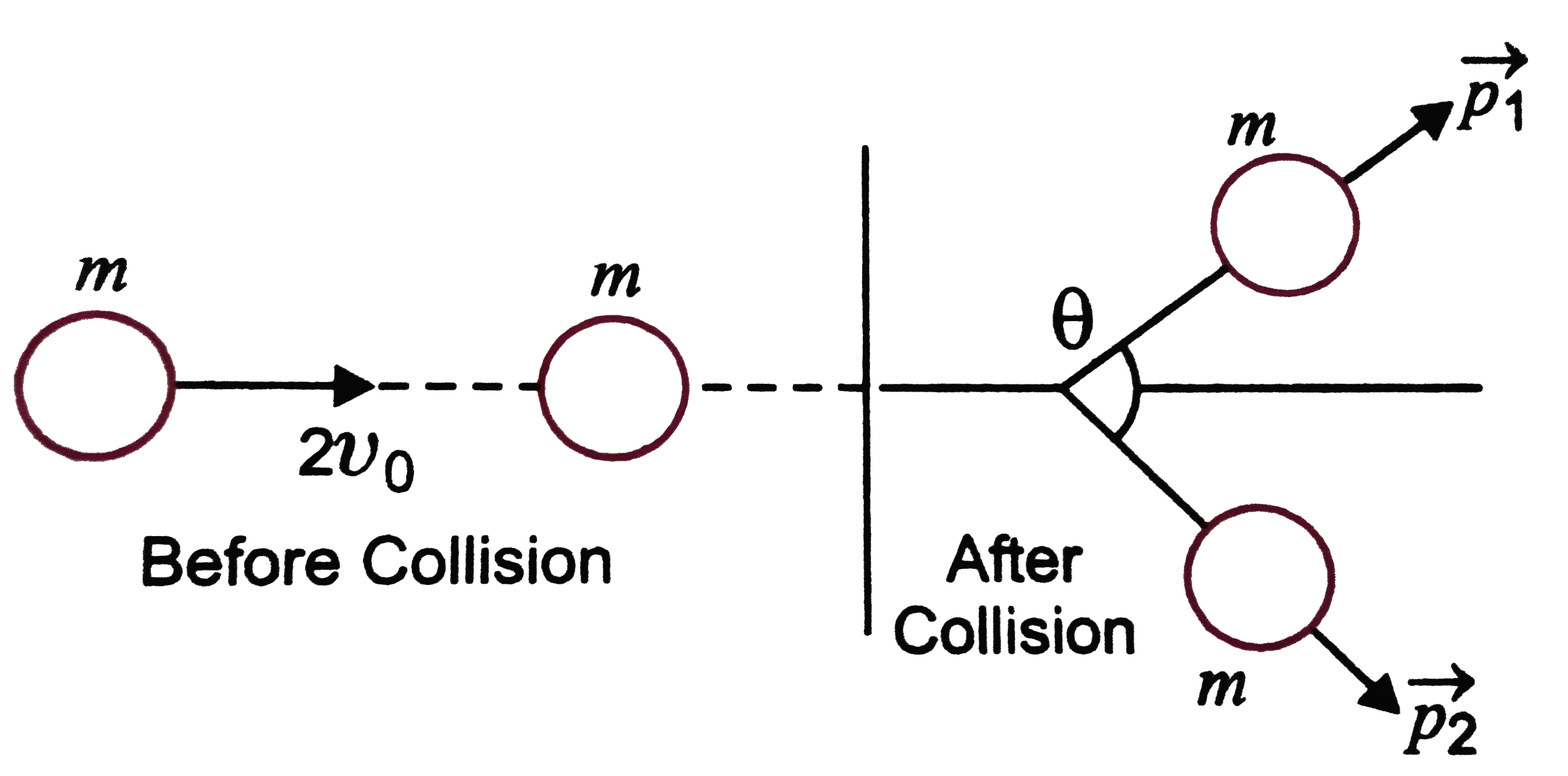
A ball of mass m$m$, moving with a speed $2{\upsilon }_0$, collides inelasticaly $(e>0)$ with an identical ball at rest. Show that $\left(a\right)$ For head - on collision, both the balls move forward.
(b) For a genergcollision, the angle between the two velocities of scattered balls is less that ${90}^{\circ }$.

Explanation

(a) If `upsilon_(1),upsilon_(2)` are velocities of two balls after collision, then according to the principle of conservation of linear momentum.
`m(2upsilon_(0))=m upsilon_(1)+m upsilon_(2)` or `2upsilon_(0)=upsilon_(1)+upsilon_(2)` …(i)
By definition, `e=(upsilon_(2)-upsilon_(1))/(upsilon_(2)+upsilon_(1))=(upsilon_(2)-upsilon_(1))/(2upsilon_(0))` `:. upsilon_(2)=upsilon_(1)+2upsilon_(0)e` ...(ii)
From (i), `2upsilon_(0)=upsilon_(1)+(upsilon_(1)+2upsilon_(0)e)`
or `=2(upsilon_(1)+upsilon_(0)e)` or `upsilon_(1)=upsilon_(0)(1-e)`
As `elt1, upsilon_(1)` has the same sign sign as `upsilon_(0)`. `:.` the ball moves forward after collision.
From (ii), `upsilon_(2)=upsilon_(0)(1-e)+2upsilon_(0)e=upsilon_(0)(1+e)`
Again, as `e lt 1, upsilon_(2)` has the same sign as `upsilon_(0)`. Hence the other ball also moves forward after collision.
(b) Accordin to principle of conservation of linear momentum,
`vec(p)=vec(p)_(1)+vec(p)_(2)`
For a general collision, some KE is lost
`:. ((p^(2))/(2m))gt ((p_(1)^(2))/(2m))+((p_(2)^(2))/(2m))`
or `p^(2)gt(p_(1)^(2)+p_(2)^(2)). `
which is possible onely when `thetalt 90^(@).` figure , which was to be proved.