Given that C denotes capacitance of a capacitor and V is the potential difference across its plates. Then the dimensions of CV2 are same as that of
momentum
power
forces
torque
The correct Answer is:D
To find the dimensions of CV2, where C is the capacitance and V is the potential difference, we can follow these steps:
1. Identify the dimensions of capacitance C:
The capacitance C is defined as the charge Q per unit potential difference V. The formula is:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The dimension of potential difference V is (M)(L2)(T−3)(I−1) (derived from the formula V=W/Q, where W is work done, and its dimension is (M)(L2)(T−2)).
Therefore, the dimension of capacitance C can be expressed as:
(C)=(Q)(V)=(I)(T)(M)(L2)(T−3)(I−1)=(M−1)(L−2)(T4)(I2)
2. Identify the dimensions of potential difference V:
As mentioned earlier, the dimension of potential difference V is:
(V)=(M)(L2)(T−3)(I−1)
3. Calculate the dimensions of V2:
To find V2, we square the dimensions of V:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
4. Combine the dimensions of C and V2:
Now we can find the dimensions of CV2:
(CV2)=(C)⋅(V2)=(M−1)(L−2)(T4)(I2)⋅(M2)(L4)(T−6)(I−2)
5. Multiply the dimensions:
When we multiply the dimensions, we combine the powers of each base unit:
(CV2)=(M−1⋅M2)(L−2⋅L4)(T4⋅T−6)(I2⋅I−2)
This simplifies to:
(CV2)=(M1)(L2)(T−2)(I0)=(M)(L2)(T−2)
6. Conclusion:
The dimensions of CV2 are the same as that of energy, which is given by:
(E)=(M)(L2)(T−2)
Final Answer:
The dimensions of CV2 are the same as that of energy.
The capacitance C is defined as the charge Q per unit potential difference V. The formula is:
C=QV
The dimension of charge Q is (I)(T) (where I is current and T is time). The dimension of potential difference V is (M)(L2)(T−3)(I−1) (derived from the formula V=W/Q, where W is work done, and its dimension is (M)(L2)(T−2)).
(C)=(Q)(V)=(I)(T)(M)(L2)(T−3)(I−1)=(M−1)(L−2)(T4)(I2)
As mentioned earlier, the dimension of potential difference V is:
(V)=(M)(L2)(T−3)(I−1)
To find V2, we square the dimensions of V:
(V2)=((M)(L2)(T−3)(I−1))2=(M2)(L4)(T−6)(I−2)
Now we can find the dimensions of CV2:
(CV2)=(C)⋅(V2)=(M−1)(L−2)(T4)(I2)⋅(M2)(L4)(T−6)(I−2)
When we multiply the dimensions, we combine the powers of each base unit:
(CV2)=(M−1⋅M2)(L−2⋅L4)(T4⋅T−6)(I2⋅I−2)
This simplifies to:
(CV2)=(M1)(L2)(T−2)(I0)=(M)(L2)(T−2)
The dimensions of CV2 are the same as that of energy, which is given by:
(E)=(M)(L2)(T−2)
The dimensions of CV2 are the same as that of energy.
Similar Questions
Knowledge Check
The displacement current flows in the dielectric of a capacitor when the potential difference across its plates-
Abecomes zeroBhas assumed a constant valueCis increasing with timeDdecreasing with timeIf V denotes te potential difference across the plate of a capacitor of capacitance C, the dimensions of CV2 are
ANot expressible in MLTBMLT−2CM2LT−1DML2T−2If L,R,C,andV, respectively , represent inductance , resistance , capacitance and potential difference , then the dimensions of L/RCV are the same as those of
AChargeB1/ChargeCCurrentD1/Current
The charge stored in a capacitor is 20μ C and the potential difference across the plates is 500V .Its capacity is ..?
View SolutionIf C be the capacitance and V be the electric potential, then the dimensional formula of CV2 is
View SolutionIf C be the capacitance and V be the electric potential, then the dimensional formula of CV2 is
View SolutionIn the circuit diagram given below, the value of the potential difference across the plates of the capacitors are.
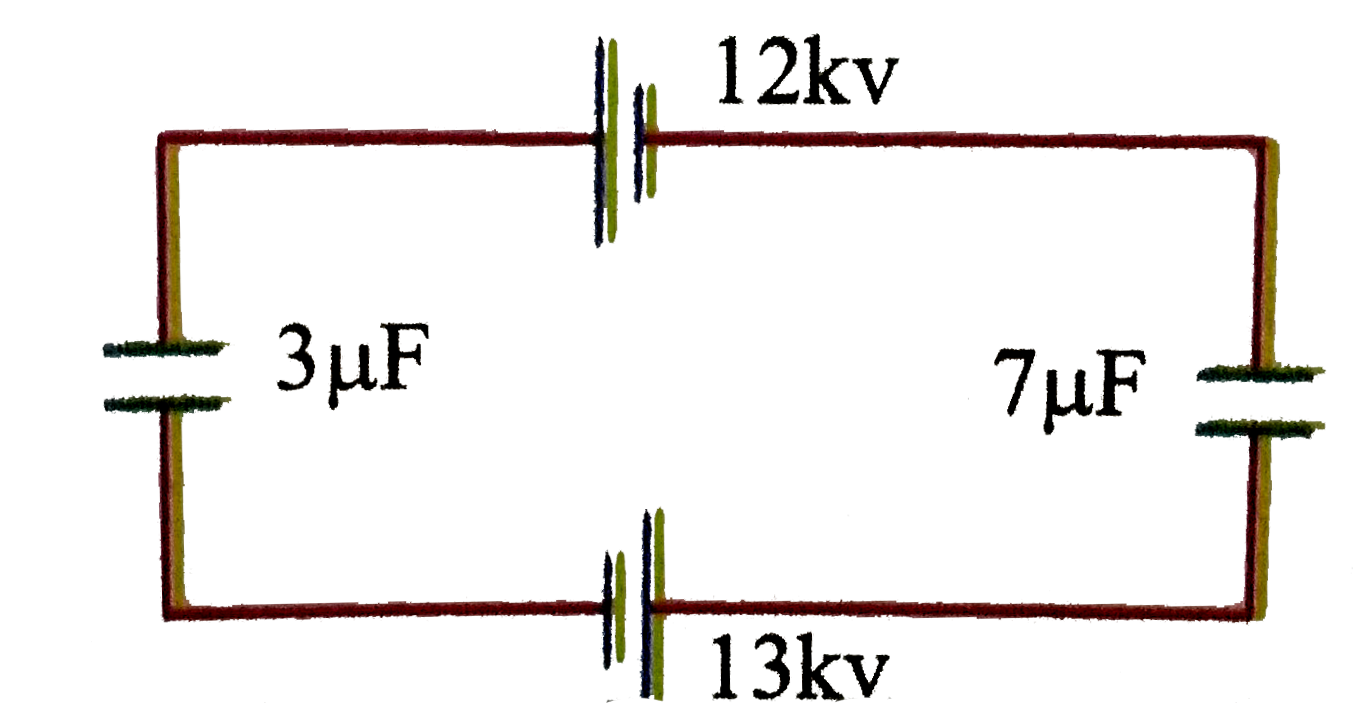 .
.
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View Solution