Find the dimension of where C= Capacitance and V is potential difference
The correct Answer is:A, B, C, D
To find the dimension of CV where C is capacitance and V is potential difference, we can follow these steps:
Step 1: Understand the relationship between charge, capacitance, and potential difference
From the definition of capacitance, we know that:
Q=CV
where Q is the charge, C is the capacitance, and V is the potential difference.
Step 2: Rearranging the equation
We can rearrange this equation to express capacitance C:
C=QV
Step 3: Substitute the expression for potential difference
The potential difference V can be expressed in terms of work W and charge Q:
V=WQ
Substituting this into the expression for capacitance gives:
C=QWQ=Q2W
Step 4: Find the expression for CV
Now, we can find CV:
CV=Q2/WW/Q=Q2W⋅QW=Q3W2
Step 5: Determine the dimensions of charge and work
The dimension of charge Q is:
(Q)=(A)(T)=A⋅T
The dimension of work W is:
(W)=(M)(L2)(T−2)=M⋅L2⋅T−2
Step 6: Substitute the dimensions into the expression
Now substituting these dimensions into our expression for CV:
CV=(A⋅T)3(M⋅L2⋅T−2)2
This simplifies to:
CV=A3⋅T3M2⋅L4⋅T−4=A3⋅T3+4M2⋅L4=A3⋅T7M2⋅L4
Step 7: Final expression for dimensions
Thus, the final dimension of CV is:
CV=M−2⋅L−4⋅T7⋅A3
Final Answer
The dimension of CV is:
(M−2⋅L−4⋅T7⋅A3)
From the definition of capacitance, we know that:
Q=CV
where Q is the charge, C is the capacitance, and V is the potential difference.
We can rearrange this equation to express capacitance C:
C=QV
The potential difference V can be expressed in terms of work W and charge Q:
V=WQ
Substituting this into the expression for capacitance gives:
C=QWQ=Q2W
Now, we can find CV:
CV=Q2/WW/Q=Q2W⋅QW=Q3W2
The dimension of charge Q is:
(Q)=(A)(T)=A⋅T
The dimension of work W is:
(W)=(M)(L2)(T−2)=M⋅L2⋅T−2
Now substituting these dimensions into our expression for CV:
CV=(A⋅T)3(M⋅L2⋅T−2)2
This simplifies to:
CV=A3⋅T3M2⋅L4⋅T−4=A3⋅T3+4M2⋅L4=A3⋅T7M2⋅L4
Thus, the final dimension of CV is:
CV=M−2⋅L−4⋅T7⋅A3
The dimension of CV is:
(M−2⋅L−4⋅T7⋅A3)
Topper's Solved these Questions
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-A
Explore 80 Videos
- JEE MAIN 2021Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2021Exercise:SECTION-B
Explore 40 Videos
- JEE MAINBook:JEE MAINS PREVIOUS YEARChapter:JEE MAINExercise:All Questions
Explore 473 Videos
- JEE MAIN 2022Book:JEE MAINS PREVIOUS YEARChapter:JEE MAIN 2022Exercise:Question
Explore 492 Videos
Similar Questions
A capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the two capacitors before they are connected .
View SolutionA capacitor of capacitance C1 is charged to a potential V1 , while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other
Find the total energy stored in the parallel combination of two capacitors.
View Solution
Knowledge Check
The dimension of 1/CR is, where C is capacitance and R is electrical resistance :
AM0L0T2BM1L2T−1A−1CM0L0T−1DM0L1T−1Given that C denotes capacitance of a capacitor and V is the potential difference across its plates. Then the dimensions of CV2 are same as that of
AmomentumBpowerCforcesDtorqueIf L,R,C,andV, respectively , represent inductance , resistance , capacitance and potential difference , then the dimensions of L/RCV are the same as those of
AChargeB1/ChargeCCurrentD1/Current
A capacitor of capacitance C1 is charged to a potential V1 while another capacitor of capacitance C2 is charged to a potential difference V2 . The capacitors are now disconnected from their respective charging batteries and connected in parallel to each other .
(a) Find the total energy stored in the two capacitors before they are connected.
(b) Find the total energy stored in the parallel combination of the two capacitors.
(c ) Explain the reason for the difference of energy in parallel combination in comparison to the total energy before they are connected.
View SolutionIn figure C1=C5=8.4μF and C2=C3=C4=4.2μF.The applied potential is Vab=220V
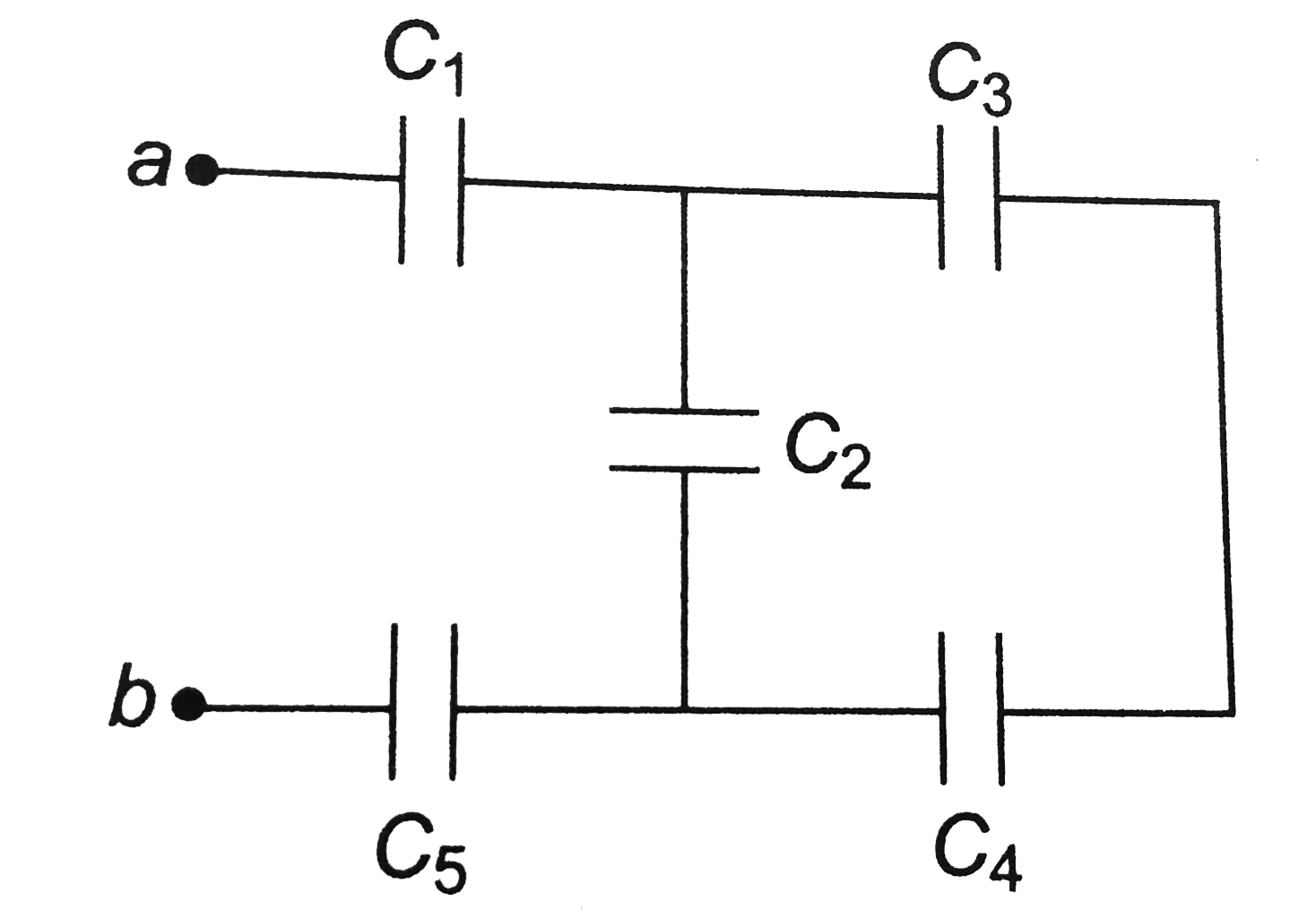
(a) What is the equivalent capacitance of the network between points a and b?
(b) Calculate the charge on each capacitor and the potential difference across each capacitor.
View SolutionA capacitor of capacitance C is charged to a potential difference V0. The charged battery is disconnected and the capacitor is connected to a capacitor of unknown capacitance Cx. The potential difference across the combination is V. The value of Cx should be
View SolutionIn the circuit shown in figure-3.345 the capacitor of capacitance C is charged to a potential difference V. The current in the circuit just after the closing of switch S is :

View SolutionA capacitor or capacitance C1 is charge to a potential V and then connected in parallel to an uncharged capacitor of capacitance C2. The fianl potential difference across each capacitor will be
View Solution

