A body moves in a straight line along x-axis, its distance from the origin is given by the equation x=8t−3t2. The average velocity in the interval from t=0 to t=4 is
2m/s
−16m/s
−4m/s
5m/s
The correct Answer is:C
To find the average velocity of a body moving along the x-axis, we can use the formula for average velocity, which is given by:
Average Velocity=Total DisplacementTotal Time
Step 1: Determine the displacement at t=0
Using the equation of motion given:
x(t)=8t−3t2
Substituting t=0:
x(0)=8(0)−3(0)2=0
Step 2: Determine the displacement at t=4
Now, substituting t=4:
x(4)=8(4)−3(4)2
Calculating this step-by-step:
1. 8(4)=32
2. 3(42)=3(16)=48
Thus,
x(4)=32−48=−16
Step 3: Calculate the total displacement
The total displacement from t=0 to t=4 is:
Displacement=x(4)−x(0)=−16−0=−16 meters
Step 4: Calculate the total time
The total time interval is:
Total Time=4−0=4 seconds
Step 5: Calculate the average velocity
Now, substituting the values into the average velocity formula:
Average Velocity=Total DisplacementTotal Time=−16 meters4 seconds=−4 m/s
Final Answer
The average velocity in the interval from t=0 to t=4 is:
Average Velocity=−4 m/s
---
2. 3(42)=3(16)=48
Similar Questions
Knowledge Check
A body moves in a straight line along Y-axis. Its distance y in metre) from the origin is given y=8t−3t2. The average speed in the time interval from t=0 second to t=1 second is
A−4ms−1BZeroC5ms−1D6ms−1A particle of mass 3 kg is moving along x - axis and its position at time t is given by equation x=(2t2+5)m. Work done by all the force acting on it in time interval t=0 to t=3s is
A144 JB72 JC108 JD216 JA body moves along x-axis such that its displacement varies with time as given, x=7+3t+5t2. The average velocity during 3rd second is
A28ms−1B42ms−1C56ms−1D15ms−1
A particle is moving in a straight line such that its distance at any time t is given by
x=t44−2t3+4t2+7. Then
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.
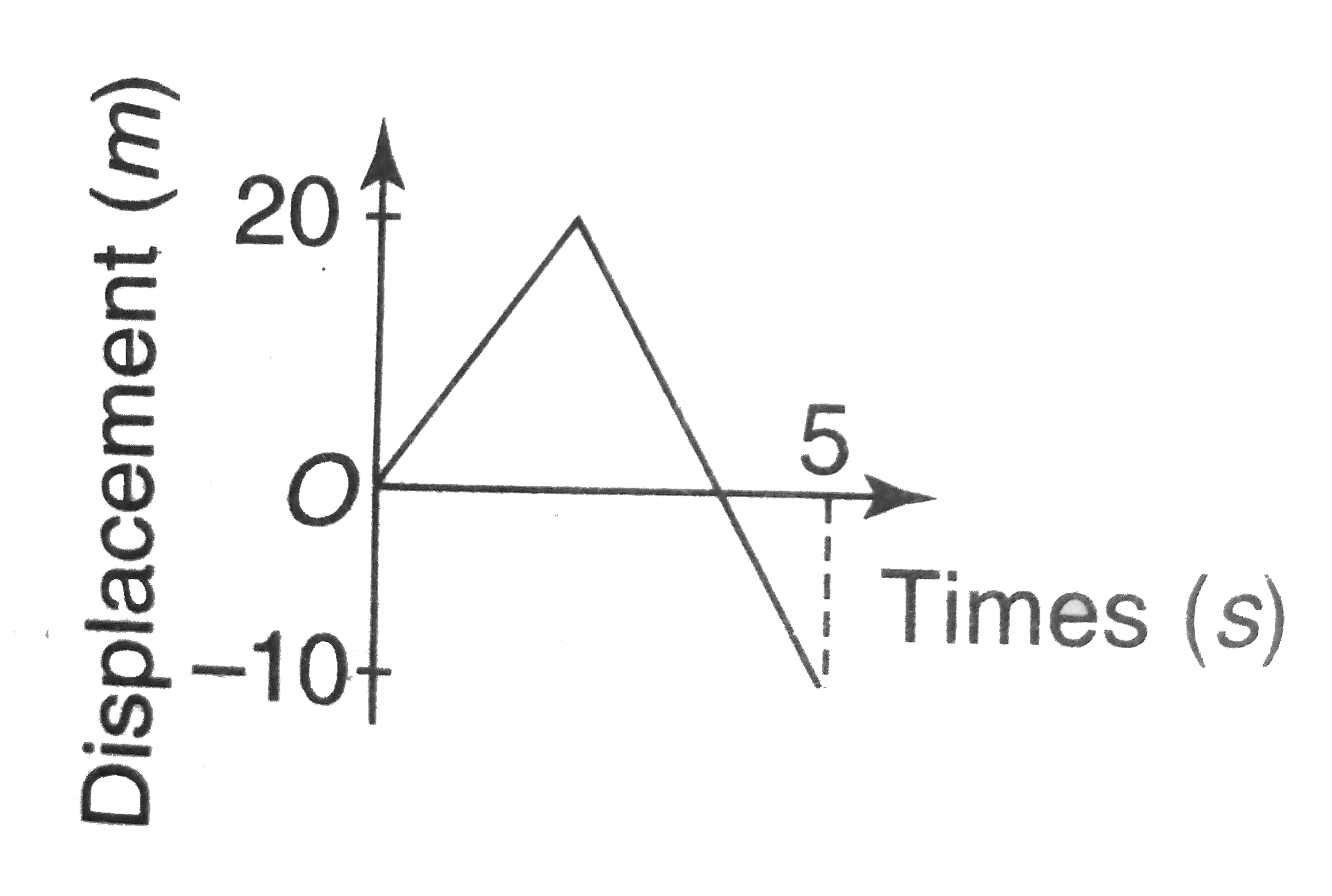
View SolutionThe diagram shows the displacement-time graph for a particle moving in a straight line. Find the average velocity for the interval from t=0 to t=5s.

View SolutionA particle is moving on a straight line and its distance x cms from a fixed point O on the line is given byx=√t2+1 then the velocity of particle at t=1 is
View SolutionThe position of a body moving along x-axis at time t is given by x=(t2−4t+6)m. The distance travelled by body in time interval t = 0 to t = 3 s is
View Solution