Forces X,Y and Z have magnitudes 10N, 5(√3−1)N and 5(√3+1)N, respectively. The forces Y and Z act in the same direction as shown in figure. The resultant of X and Y and the resultant of X and Z have the same magnitudes. Find θ, the angle between X and Y.

150∘
135∘
120∘
105∘
The correct Answer is:A
Step by step video & text solution for Forces X,Y and Z have magnitudes 10N, 5(sqrt(3)-1) N and 5(sqrt(3)+1) N, respectively. The forces Y and Z act in the same direction as shown in figure. The resultant of X and Y and the resultant of X and Z have the same magnitudes. Find theta, the angle between X and Y. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
Knowledge Check
Two forces of magnitude 1 N and 13 N resultant of magnitude 6√5N, then that is the angle between two forces.
Acos−1.113Bcos−1.513Ccos−1.135Dcos−1.137The two forces 2√2N and xN are acting at a point their resultant is perpendicular to ˆxN and having magnitude of √6N.The angle between the two forces and magnitude of x are.
Aθ=120∘,X=√2NBθ=30∘,X=√2NCθ=150∘,X=√3NDθ=150∘,X=√2NIf two forces of 5 N each are acting along X and Y axes, then the magnitude and direction of resultant is
A5√2,π/3B5√2,π/4C−5√2,π/3D−5√2,π/4
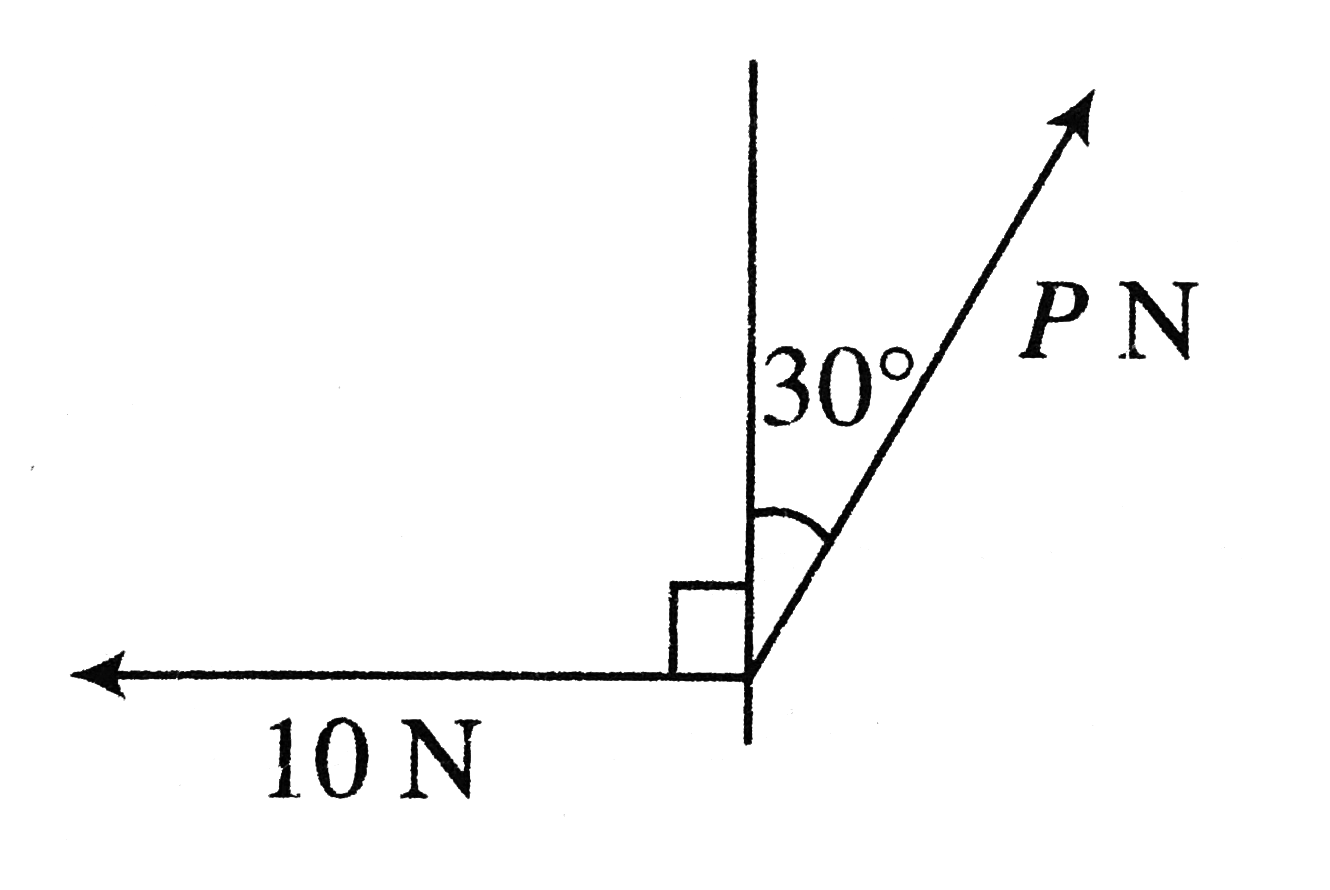
Two horizontal forces of magnitudes of 10N and PN act on a particle. The force of magnitude 10N acts due west and the force of magnitude PN acts on a bearing of 30∘ east of north as shown in (figure) The resultant of these two force acts due north. Find the magnitude of the resultant.
View SolutionThe magnitudes of two forces X and Y are in the ratio 2:3 . If the resultant of two forces is 25N and angle between them 60∘, find the magnitude of each force close to one place of decimal .
View SolutionThree ant P,Q and R are pulling a grain with forces of magnitude 6N,3√3N and 3√2N as shown in the figure. Find the magnitude of resultant force (in N ) acting on the grain .

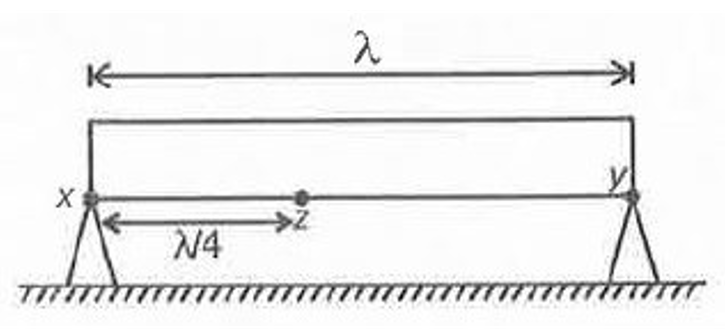
View SolutionA uniform plank is supported by two equal 120 N forces at x and y as shown in figure. If the support at x is moved to z, then the supporting forces at y and z are
View SolutionFind the angle between the plane: x−y+z=5 and x+2y+z=9
View Solution
