Two closed containers of equal volume of air are initially at 1.05×105 Pa, and 300 K temperature. If the containers are connected by a narrow tube and one container is maintained at 300 K temperature and other at 400 K temperature. Find the final pressure in the containers.
To solve the problem step by step, we will use the ideal gas law and the concept of conservation of moles.
Step 1: Understand the Initial Conditions
We have two containers of equal volume (let's denote the volume of each container as V) filled with air at an initial pressure P0=1.05×105 Pa and temperature T0=300 K.
Step 2: Calculate the Initial Number of Moles
Using the ideal gas law, we can find the initial number of moles n in each container:
PV=nRT
For one container, we have:
n=P0VRT0
Substituting the values:
n=(1.05×105)VR⋅300
Step 3: Set Up the Final Conditions
When the containers are connected by a narrow tube, one container is kept at T1=300 K and the other at T2=400 K. Let PF be the final pressure in both containers when equilibrium is reached.
Step 4: Calculate the Number of Moles in Each Container at Final Conditions
For the container at T1=300 K:
n1=PFVR⋅300
For the container at T2=400 K:
n2=PFVR⋅400
Step 5: Apply the Conservation of Moles
The total number of moles before connecting the containers must equal the total number of moles after they are connected:
n=n1+n2
Substituting the expressions for n, n1, and n2:
(1.05×105)VR⋅300=PFVR⋅300+PFVR⋅400
Step 6: Simplify the Equation
Cancel V and R from both sides:
1.05×105=PF300+PF400
Finding a common denominator (which is 1200):
1.05×105=4PF+3PF1200
1.05×105=7PF1200
Step 7: Solve for PF
Rearranging the equation gives:
PF=1.05×105×12007
Calculating the right-hand side:
PF=1.26×1087≈1.8×107 Pa
Converting to kilopascals:
PF≈120 kPa
Final Answer
The final pressure in the containers is PF=120 kPa.
---
We have two containers of equal volume (let's denote the volume of each container as V) filled with air at an initial pressure P0=1.05×105 Pa and temperature T0=300 K.
Using the ideal gas law, we can find the initial number of moles n in each container:
PV=nRT
For one container, we have:
n=P0VRT0
Substituting the values:
n=(1.05×105)VR⋅300
When the containers are connected by a narrow tube, one container is kept at T1=300 K and the other at T2=400 K. Let PF be the final pressure in both containers when equilibrium is reached.
For the container at T1=300 K:
n1=PFVR⋅300
For the container at T2=400 K:
n2=PFVR⋅400
The total number of moles before connecting the containers must equal the total number of moles after they are connected:
n=n1+n2
Substituting the expressions for n, n1, and n2:
(1.05×105)VR⋅300=PFVR⋅300+PFVR⋅400
Cancel V and R from both sides:
1.05×105=PF300+PF400
Finding a common denominator (which is 1200):
1.05×105=4PF+3PF1200
1.05×105=7PF1200
Rearranging the equation gives:
PF=1.05×105×12007
Calculating the right-hand side:
PF=1.26×1087≈1.8×107 Pa
Converting to kilopascals:
PF≈120 kPa
The final pressure in the containers is PF=120 kPa.
Topper's Solved these Questions
- Kinetic Theory of Gases and Gas LawsBook:PHYSICS GALAXY - ASHISH ARORAChapter:Kinetic Theory of Gases and Gas LawsExercise:Discussion Question
Explore 18 Videos
- Kinetic Theory of Gases and Gas LawsBook:PHYSICS GALAXY - ASHISH ARORAChapter:Kinetic Theory of Gases and Gas LawsExercise:Conceptual MCQs Single Option Correct
Explore 27 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:PHYSICS GALAXY - ASHISH ARORAChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:U.N.P
Explore 79 Videos
Similar Questions
Two closed vessels of equal volune contain air at 105kPa, 300K and are connected through a narrow tube. If one of the vessels is mow maintained at 300K and the other at 400K, what will be the pressure in the vessels?
View SolutionTwo closed vessels of equal volume contain air at P0 pressure, T0 temperature and are connected through a narrow tube, If one of the vessels is now maintained at T0 and other at T, what will be the pressure in the vessels?
View Solution
Knowledge Check
Two closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
A2P1T1T1+T2BT12P1T2C2P1T2T1+T2D2P1T1+T2Two closed vessels of equal volume containing air at pressure P1 and temperature T1 are connected to each other through a narrow tube. If the temperature in one of the vessels is now maintained at T1 and that in the other at T2, what will be the pressure in the vessels?
A2P1T1T1+T2BT12P1T2C2P1T2T1+T2D2P1T1+T2Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:
 A2p,(T2T1+T2)B2p,(T1T2T1+T2)Cp,(T1T2T1+T2)D2p,(T1T1+T2)
A2p,(T2T1+T2)B2p,(T1T2T1+T2)Cp,(T1T2T1+T2)D2p,(T1T1+T2)
Two closed bulbs of equal volume (V) containing an ideal gas initially at pressure pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure pf is:

View SolutionA glass container encloses a gas a pressure of 8×105 pa and 300 K temperature. The container walls can bear a maximum pressure of 106 Pa. If the temperature of container is gradually increased, find the temperature at which the container will break.
View SolutionTwo closed bulbs of equal volume (V) containing an ideal gas initially at pressure Pi and temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then raised to T2. The final pressure Pf is :

View SolutionTwo closed bulb of euqal volume (V) containing an ideal gas initially at pressure pi and Temperature T1 are connected through a narrow tube of negligible volume as shown in the figure below. The temperature of one of the bulbs is then released to T2. The final pressure pt is :
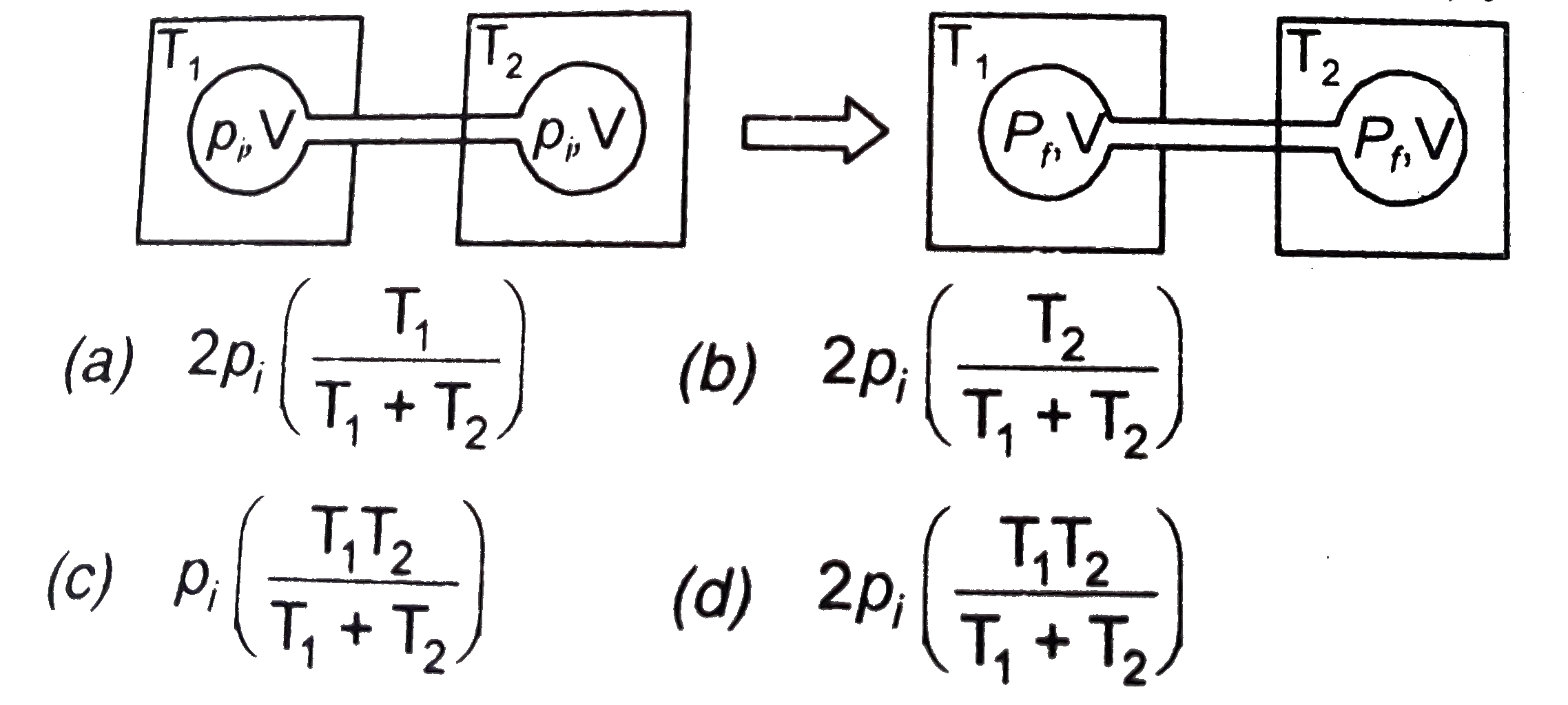
View SolutionA glass container encloses gas at a pressure 4×105 Pa and 300 K temperature. The container walls can bear a maximum pressure of 8×105 Pa. If the temperature of container is gradually increased find temperature at which container will break.
View Solution

