The temperature of a room of volume Vrise from T1 to T2. How much will the mass of the air in the room changes if the atmospheric pressure is p0. The molecular weight of the air is M.
To solve the problem of how the mass of air in a room changes as the temperature rises from T1 to T2 while maintaining constant atmospheric pressure p0, we can use the ideal gas law. The ideal gas law states:
PV=nRT
Where:
- P is the pressure,
- V is the volume,
- n is the number of moles,
- R is the universal gas constant,
- T is the temperature in Kelvin.
Given:
- The volume of the room V is constant.
- The atmospheric pressure p0 is constant.
- The molecular weight of air is M.
Step 1: Calculate the initial mass of air (m1) at temperature T1
Using the ideal gas law, we can express the number of moles n in terms of mass m and molecular weight M:
n=mM
Substituting this into the ideal gas equation gives:
p0V=m1MRT1
Rearranging for m1:
m1=p0VMRT1
Step 2: Calculate the final mass of air (m2) at temperature T2
Similarly, for the final state at temperature T2:
p0V=m2MRT2
Rearranging for m2:
m2=p0VMRT2
Step 3: Calculate the change in mass (Δm)
The change in mass Δm can be found by subtracting the initial mass from the final mass:
Δm=m2−m1
Substituting the expressions for m1 and m2:
Δm=p0VMRT2−p0VMRT1
Factoring out the common terms:
Δm=p0VMR(1T2−1T1)
Final Result
Thus, the change in mass of the air in the room as the temperature rises from T1 to T2 is given by:
Δm=p0VMR(1T2−1T1)
---
- P is the pressure,
- V is the volume,
- n is the number of moles,
- R is the universal gas constant,
- T is the temperature in Kelvin.
- The volume of the room V is constant.
- The atmospheric pressure p0 is constant.
- The molecular weight of air is M.
Topper's Solved these Questions
- Kinetic Theory of Gases and Gas LawsBook:PHYSICS GALAXY - ASHISH ARORAChapter:Kinetic Theory of Gases and Gas LawsExercise:Advance MCQs with One or More Options Correct
Explore 15 Videos
- HEAT TRANSFER Book:PHYSICS GALAXY - ASHISH ARORAChapter:HEAT TRANSFER Exercise:Unsolved Numerical Problems for Preparation of NSEP,INPhO&IPhO
Explore 66 Videos
- MAGNETIC EFFECTS OF CURRENT AND MAGNETISMBook:PHYSICS GALAXY - ASHISH ARORAChapter:MAGNETIC EFFECTS OF CURRENT AND MAGNETISMExercise:U.N.P
Explore 79 Videos
Similar Questions
Find the internal energy of air in a room of volume 40m3 at 1 standard atmospheric pressure.
View SolutionAir is filled inside a jar which has a pressure gauge connected to it. The temperature of the air inside the jar is same as outside temperature (=T0) but pressure (P1) is slightly larger than the atmospheric pressure (P0). The stopcock is quickly opened and quickly closed, so that the pressure inside the jar becomes equal to the atmospheric pressure P0. The jar is now allowed to slowly warm up to its original temperature T0. At this time the pressure of the air inside is P2(P0<P2<P1). Assume air to be an ideal gas. Calculate the ratio of specific heats (=γ) for the air, in terms of P0,P1 and P2.
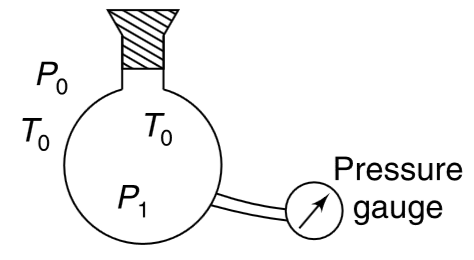
View Solution
Knowledge Check
Assume that the temperature remains essentially constant in the upper parts of the atmosphere. The atmospheric pressure varies with height as. (the mean molecular weight of air is M, where P0= atmospheric pressure at ground reference)
APe−3Mgh2RTBP0e−Mgh2RTCP0e−3MghRTDP0eMghRTThe temperature of an open room of volume 30m3 increases from 17∘C→27∘C due to sunshine. The atmospheric pressure in the room remains 1×105Pa. If niandnf are the number of molecules in the room before and after heating then nf and ni will be
A2.5×1025B−2.5×1025C−1.61×1023D1.38×1023A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless postion.
 The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be A2poABpoACpoA2DpoA
The pistons are connected to each other by a metallic wirte. Initially the pressure of the gas is po and temperature is To, atmospheric pressure is also po Now the temperature of the gas is increased to 2T0, the tension in the wire will be A2poABpoACpoA2DpoA
Call the (rms) speed of the molecules in an ideal gas V0 at temperature T0 and pressure p0. Find the speed if (a) the temperature id raised from T0=293Kto573K (b) the pressure is doubled and T=T0 ( c) the molecular weight of each of the gas molecules is tripled.
View Solution
A cylindrical tube of uniform cross-sectional area A is fitted with two air tight frictionless pistons. The pistons are connected to each other by a metallic wire. Initially the pressure of the gas is P0 and temperature is T0, atmospheric pressure is also P0. Now the temperature of the gas is increased to 2T0, the tension in the wire will be
View SolutionTwo mole of Hydrogen and three mole of Helium are mixed at room temperature and at atmospheric pressure Pa and the mixture occupies a volume V.
View SolutionThe molar specific heat of air at room temperature and 1 atm pressure is 25JK−1mol−1. How much heat is required to heat the room through 10 kelvin at room temperature if 144g of air is present in room ? Vapour density of air =14.4
View SolutionAt room temperature the ratio of velocity of sound in air at 10 atmospheric pressure to the at 1 atmospheric pressure will be
View Solution