A glass container encloses gas at a pressure 4×105 Pa and 300 K temperature. The container walls can bear a maximum pressure of 8×105 Pa. If the temperature of container is gradually increased find temperature at which container will break.
600K
150K
1200K
375K
The correct Answer is:A
To solve the problem, we will use the ideal gas law and the relationship between pressure and temperature when the volume is constant.
1. Identify Given Values:
- Initial Pressure, P1=4×105 Pa
- Initial Temperature, T1=300 K
- Maximum Pressure, P2=8×105 Pa
2. Use the Ideal Gas Law:
Since the volume of the container is constant, we can use the relationship derived from the ideal gas law which states that for a fixed volume, the ratio of pressure to temperature remains constant:
P1T1=P2T2
3. Substitute the Known Values:
Plugging in the known values into the equation:
4×105300=8×105T2
4. Cross-Multiply to Solve for T2:
Cross-multiplying gives:
4×105⋅T2=8×105⋅300
5. Calculate the Right Side:
Calculate 8×105⋅300:
8×105⋅300=240×105=2.4×107
6. Isolate T2:
Now, divide both sides by 4×105:
T2=2.4×1074×105
7. Perform the Division:
T2=2.44×107−5=0.6×102=60
Therefore, T2=600 K.
Final Answer:
The temperature at which the container will break is T2=600 K.
---
- Initial Pressure, P1=4×105 Pa
- Initial Temperature, T1=300 K
- Maximum Pressure, P2=8×105 Pa
Since the volume of the container is constant, we can use the relationship derived from the ideal gas law which states that for a fixed volume, the ratio of pressure to temperature remains constant:
P1T1=P2T2
Plugging in the known values into the equation:
4×105300=8×105T2
Cross-multiplying gives:
4×105⋅T2=8×105⋅300
Calculate 8×105⋅300:
8×105⋅300=240×105=2.4×107
Now, divide both sides by 4×105:
T2=2.4×1074×105
T2=2.44×107−5=0.6×102=60
Therefore, T2=600 K.
The temperature at which the container will break is T2=600 K.
Similar Questions
A glass container encloses a gas a pressure of 8×105 pa and 300 K temperature. The container walls can bear a maximum pressure of 106 Pa. If the temperature of container is gradually increased, find the temperature at which the container will break.
View SolutionTwo closed containers of equal volume of air are initially at 1.05×105 Pa, and 300 K temperature. If the containers are connected by a narrow tube and one container is maintained at 300 K temperature and other at 400 K temperature. Find the final pressure in the containers.
View Solution
Knowledge Check
A 0.50 L container is ocupied by nitrogen at a pressure of 800 torr and a temperature of 0∘C. The container can only withstand a pressure of 3.0 atm. What is the highest temperature (∘C) to which the container may be heated?
A505B450C625D560A vessel contains a gas under a pressure of 5×105pa. If 3/5 of the mass of the gas is flown out, What will be the gas pressure if the temperature being maintained constant,
A50MPaB2MPaC0.2MPaD0.5MPaThe temperature of a gas contained in a closed vessel increases by 1∘C when pressure of the gas is increased by 1%. The initial temperature of the gas is
A100 KB100∘CC250KD250∘C
An LPG cylinder contains gas at a pressure of 300 kPa at 27∘C. The cylinder can withstand the pressure of 1.2×106Pa. The room in which the cylinder is kept catches fire. The minimum temperature at which the bursting of cylinder will take place is __________ ∘C. (Nearest integer)
View SolutionAn iron cylinder contains helium at a pressure of 250kPa at 300K. The cylinder can withstand a pressure of 1×105Pa. The room in which the cylinder is placed catches fire. Predict whether the cylinder will blow before it melts or not (m.p of cylinder =1800K)
View SolutionA gas cylinder has walls that can bear a maximum pressure of 1.0×106Pa. It contains a gas at 8.0×105Pa and 300K. The cylinder is steadily heated. Neglecting any change in the volume calculate the temperature at which the cylinder will break.
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
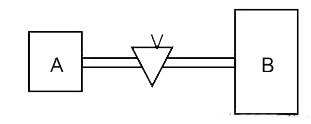
The valve V is adjusted to allow the pressure to equalize, but the temperature of each container is kept constant at the initial value, then the pressure in the two containers is :
View SolutionContainer A holds an ideal gas at a pressure 1×105 Pa and at 300 K. Container B whose volume is 4 times the volume of A has the same ideal gas at 400 K and at a pressure of 5×105
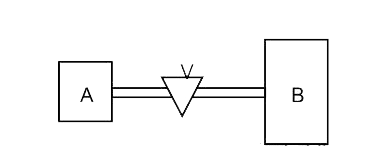
Before the valve V is opened, VA and VB are rms velocities of the molecules in container A and B then VAVB is:
View Solution
