For the first-order reaction (C=C0e−kt1) and Tav=k−11. After two average lives concentration of the reactant is reduced to :
0.25
0.75
100e%
100e2%
The correct Answer is:D
C=Coe−k1t After t=2k1[1/k1 is called average life]⇒C=Coe−2=Coe2=100e2%
Similar Questions
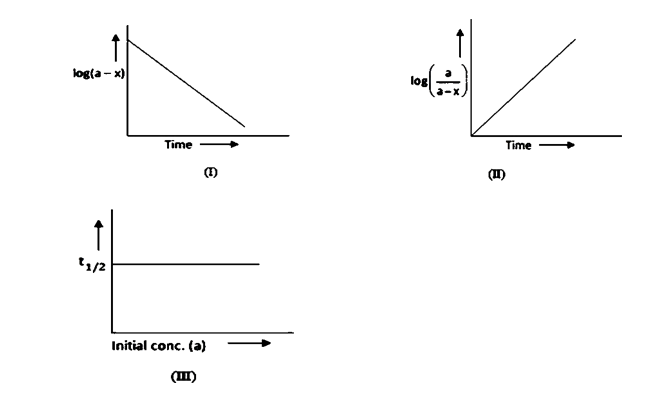
Which of the following is/are correct for the first order reaction ? (a is initial concentration of reactant, x is concentration of the reactant reacted and t is time)
View SolutionThe rate for a first order reaction is 0.6932×10−2molL−1min−1 and the initial concentration of the reactants is 1M, T1/2 is equal to
View Solution
Knowledge Check
Concentration of the reactant in first order is reduced to 1e2 after
Aone natural life timeBtwo natural life timeCthree natural life timeDfour natural life timeFor the first-order reaction Tav (average life), T50 and T75 in the increasing order are :
AT50<Tav<T75BT50<T75<TavCTav<T50<T75DTav=T50<T75For the first-order reaction Tav (average life), T50 (half-life) and T75 (time 75% reaction) are in the ratio of
A1.44:2:3B1.44:1:2C1:2:1.44D1:2:3
The rate for a first order reaction is 0.6932×10−2molL−1min−1 and the initial concentration of the reactants is 1M, T1/2 is equal to
View SolutionAt T (K) , if the rate constant of a first order reaction is 4.606×10−3s−1, the time to reduce the initial concentration of the reactant to 110 in seconds is :
View SolutionFor a zero order reaction,
K=1×10−3mol L−1s−1
If initial concentration of the reactant is 1.0mol L−1 , the concentration after 10 minutes would be
View SolutionGiven that for a reaction of nth order, the integrated rate equation is:
K=1t(n−1)[1Cn−1−1Cn−10], where C and C0 are the concentration of reactant at time t and initially respectively. The t3/4 and t1/2 are related as t3/4 is time required for C to become C1/4) :
View SolutionIn the Wilhelmey equation of a first order reaction ct=c0e−kt. If the initial concentration c0 is increased m times, then
View Solution
