For the consecutive unimolecular-type first-order reaction $A k_{1} - - \to R k_{2} - - \to S$ , the concentration of component R, $C_{R}$ at any time $t$ is given by -
$C_{R} = C_{O A} K_{1} [\frac{e_{1}^{- k_{1} t}}{(k_{2} - k_{1})} + \frac{e_{2}^{- k_{2} t}}{(k_{1} - k_{2})}]$
if $C_{A} = C_{A O}, C_{R} = C_{R O} = 0$ at $t = 0$
The time at which the maximum concentration of $R$ occurs is -

$t_{max} = \frac{k_{2} - k_{1}}{ln (k_{2} / k_{1})}$

$t_{max} = \frac{ln (k_{2} / k_{1})}{k_{2} - k_{1}}$

$t_{max} = \frac{e_{2}^{k_{2} / k_{1}}}{k_{2} - k_{1}}$

$t_{max} = \frac{e_{2}^{k_{2} - k_{1}}}{k_{2} - k_{1}}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

For the consecutive unimolecular first order reaction $A k_{1} - - \to R k_{2} - - \to S$ , the concentration of component $A$ , $C_{A}$ at any time $t$ is given by
A $C_{=} C_{A_{0}} e^{(k_{1} + k_{2}) t}$
B $C_{A} = C_{A_{0}} e^{- (k_{1} + k_{2}) t}$
C $C_{A} = C_{A_{0}} e_{1}^{- k_{1} t}$
D $C_{A} = C_{A_{0}} e_{1}^{k_{1} t}$
A consecutive reaction, $A K_{1} - - \to B K_{2} - - \to C$ is characterised by:
AMaximum in the concentration of $A$
BMaximum in the concentration of $B$
CMaximum in the concentration of $C$
DHighly exothermicity
For the two step reaction in which both the steps are first order

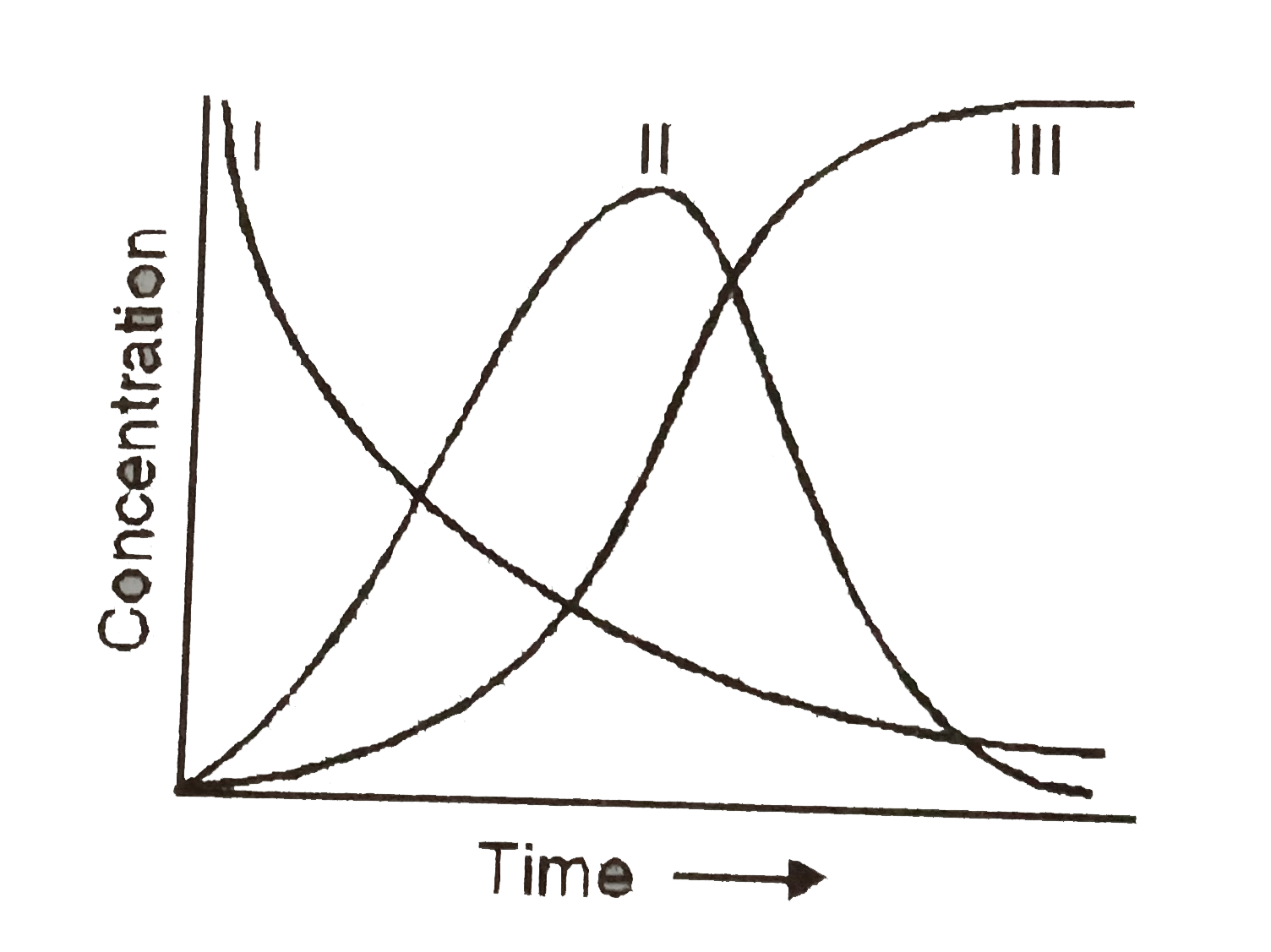
$R k_{1} - - \to I$
$I k_{2} - - \to P$
the rate of change of concentration of I is given by the plot
AI
BII
CIII
DNone