Two consecutive irreversible fierst order reactions can be represented by
A → k 1 B → k 2 C
The rate equation for A is readily interated to obtain
[ A ] t = [ A ] 0 . e - k 1 t , and [ B ] t = k 1 [ A ] 0 k 2 - k 1 [ e - k 1 t - e - k 2 t ]
At what time will B be present in maximum concentration ?

A

K 1 K 2 - K 1

B

1 k 1 - k 2 In k 1 ) k 2

C

1 k 2 - k 1 In k 1 ) k 2

D

none of these

Video Solution
Doubtnut Promotions Banner
Text Solution
Generated By DoubtnutGPT

The correct Answer is:B

To find the time at which the concentration of B is at its maximum in the consecutive irreversible first-order reactions represented by:

Ak1→Bk2→C

we can follow these steps:

Step 1: Write the expression for the concentration of B

The concentration of B at time t is given by:

(B)t=k1(A)0k2−k1(e−k1t−e−k2t)

Step 2: Differentiate the concentration of B with respect to time

To find the time at which B is at maximum concentration, we need to differentiate (B)t with respect to time t and set the derivative equal to zero:

d(B)dt=0

Differentiating (B)t:

d(B)dt=k1(A)0k2−k1(−k1e−k1t+k2e−k2t)

Step 3: Set the derivative equal to zero

Setting the derivative equal to zero gives us:

−k1e−k1t+k2e−k2t=0

Rearranging this equation, we have:

k1e−k1t=k2e−k2t

Step 4: Divide both sides by e−k2t

Dividing both sides by e−k2t:

k1e(k2−k1)t=k2

Step 5: Solve for t

Taking the natural logarithm of both sides:

ln(k1)+(k2−k1)t=ln(k2)

Rearranging gives:

(k2−k1)t=ln(k2)−ln(k1)

Thus,

t=ln(k2)−ln(k1)k2−k1

This can also be expressed as:

t=1k2−k1ln(k2k1)

Final Answer

The time at which B is present in maximum concentration is:

tmax=1k2−k1ln(k2k1)

---

Updated on:7/8/2024
|
Class 12CHEMISTRYCHEMICAL KINETICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Two consecutive irreversible fierst order reactions can be represented by
    Ak1−−→Bk2−−→C
    The rate equation for A is readily interated to obtain
    [A]t=[A]0.e−k1t , and [B]t=k1[A]0k2−k1[e−kt1−e−kt2]
    Select the corret statement for given reaction:

    AA decreases linearly
    BB rise to a max. and then constant
    CB rises to a max and the falls
    DThe slowest rate of increases of C occuring where B is max

  • Two consecutive irreversible fierst order reactions can be represented by
    Ak1−−→Bk2−−→C
    The rate equation for A is readily interated to obtain
    [A]t=[A]0.e−k1t , and [B]t=k1[A]0k2−k1[e−kt1−e−kt2]
    If k1 and k2 both are almost same then which graph is most suitable ?

    Agraph A
    Bgraph B
    Cgraph C
    Dgraph D

  • Two consecutive irreversible fierst order reactions can be represented by
    Ak1−−→Bk2−−→C
    The rate equation for A is readily interated to obtain
    [A]t=[A]0.e−k1t , and [B]t=k1[A]0k2−k1[e−kt1−e−kt2]
    When k1=1s−1 and k2=500s−1 , select most appropriate graph

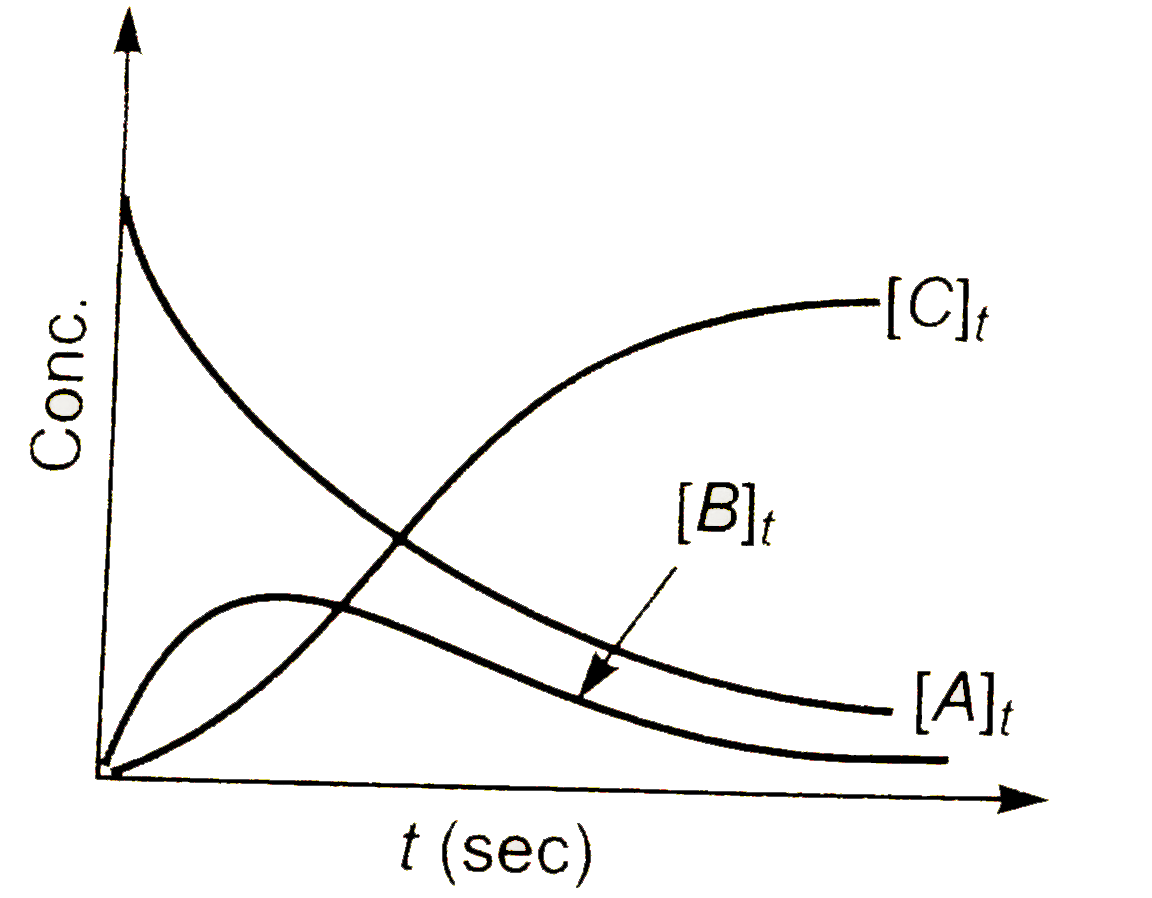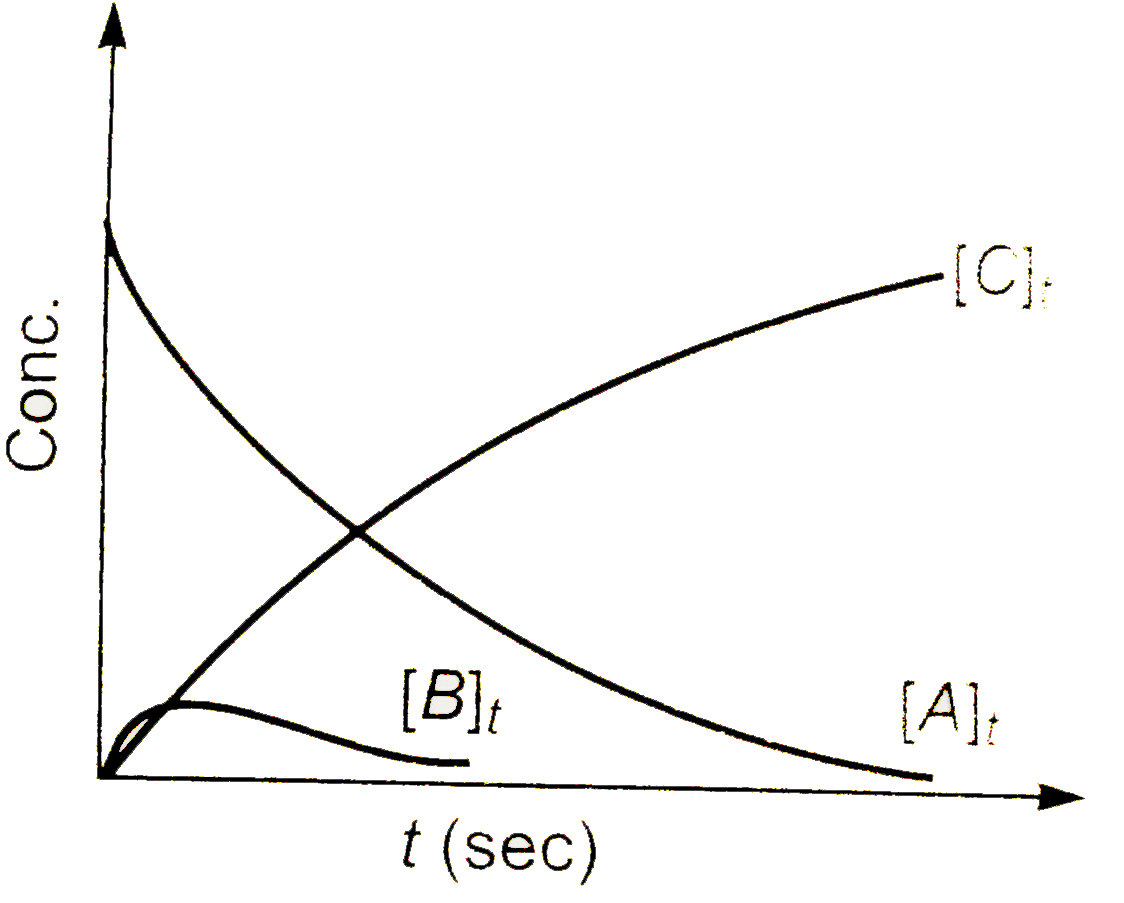    Aocr_image
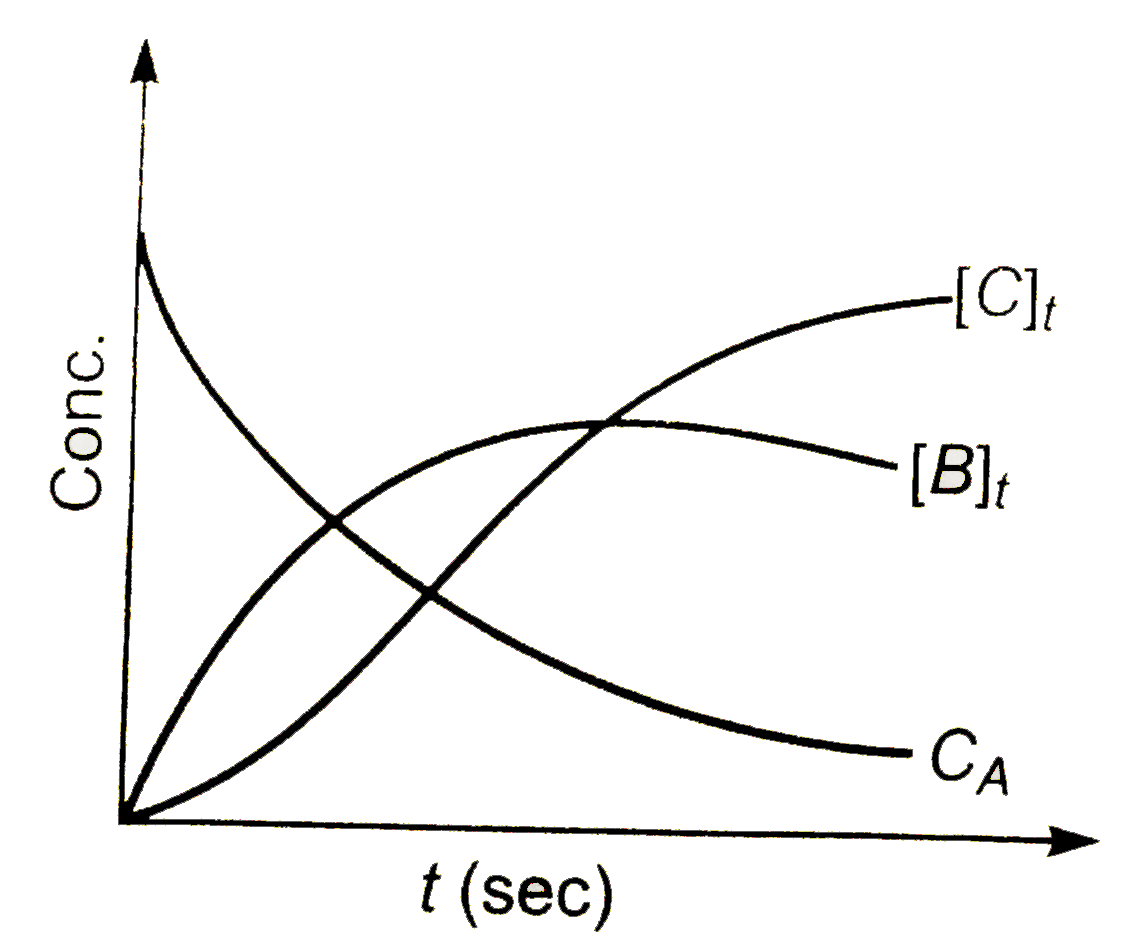    Bocr_image
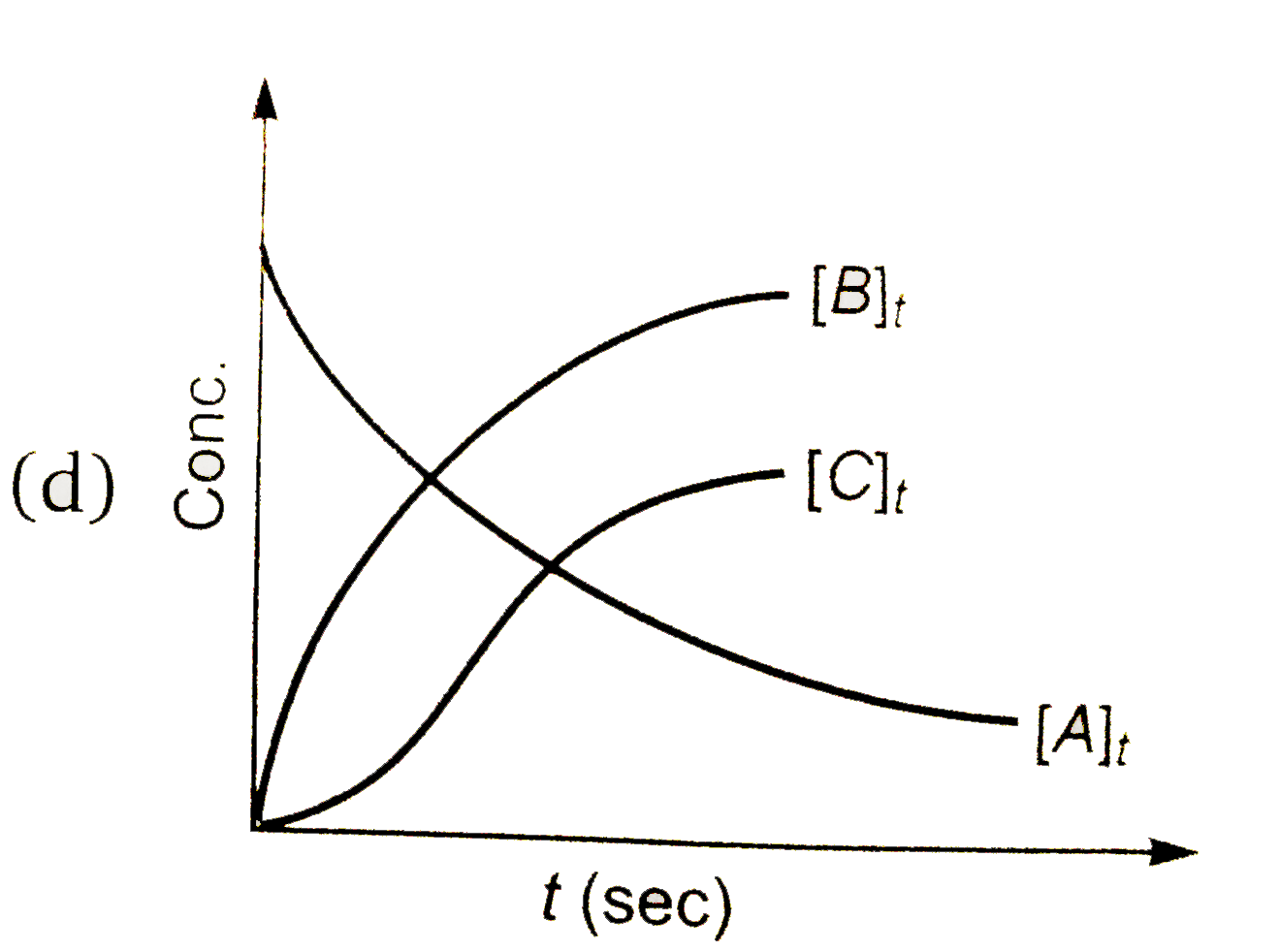
    Cocr_image
    Docr_image