Two point charges $q_{1} (\sqrt{10} μ C)$ and $q_{2} (- 25 μ C)$ are placed on the x-axis at x = 1 m and x = 4 m respectively. The electric field (in V/m) at a point y =3 m on y-axis is,
$[take \frac{1}{4 π \in_{0}} = 9 \times 10^{9} N m^{2} C^{- 2}]$

A

$(63 ˆ i - 27 ˆ J) \times 10^{2}$

B

$(- 81 ˆ i + 81 ˆ J) \times 10^{2}$

C

$(- 63 ˆ i + 27 ˆ J) \times 10^{2}$

D

$(81 ˆ i - 81 ˆ J) \times 10^{2}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

$e = {\to E}_{1} + {\to E}_{2}, = 9 \times 10^{9} {\frac{q_{1}}{A P^{3}}} (- ˆ i + 3 ˆ j) + \frac{q_{2}}{B P^{3}} (- 4 ˆ i + 3 ˆ j)$
$= 9 \times 10^{9} {\frac{\sqrt{10} \times 10^{- 6}}{10 \sqrt{10}} (- ˆ i + 3 ˆ j) + \frac{25}{25 + 5} (- 4 ˆ i + 3 ˆ j)}$
$= (63 i - 27 j) \times 10^{2})$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
Point charge $q_{1} = 2 μ C$ and $q_{2} = - 1 μ C$ are kept at points $x = 0$ and $x = 6$ respectively. Electrical potential will be zero at points
A $x = 2 and x = 9$
B $x = 1 and x = 5$
C $x = 4 and x = 12$
D $x = - 2 and x = 2$
Question 2 - Select One
Two point charges $q_{1} = 4 μ C$ and $q_{2} = 9 μ C$ are placed $20 c m$ apart. The electric field due to them will be zero on the line joining them at distamce of
A $8 c m$ from $q_{1}$
B $8 c m$ from $q_{2}$
C $\frac{80}{13} c m$ from $q_{1}$
D $\frac{80}{13} c m$ from $q_{2}$
Question 3 - Select One
Two point charges $q_{1} and q_{2}$ , of magnitude $+ 10^{- 8} C and - 10^{- 8} C$ , respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.

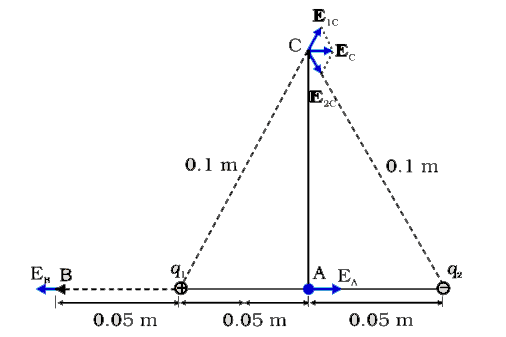A $E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the RIGHT.
B $E_{A} = 7.2 \times 10^{- 4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the left.
C $E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the left.
D $E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{- 4} N C^{- 1}$
$E_{B}$ is directed towards the left.

Recommended Questions

Home
Ask Doubt
Profile