Two charges of 4μC each are placed at the corners A and B of an equilaternal triangle of side length 0.2m in air. The
electric potential at C is [14πε0=9×109N−m2C2]
9×104V
18×104V
36×104V
36×104V
The correct Answer is:C
To find the electric potential at point C due to the two charges placed at points A and B in an equilateral triangle, we can follow these steps:
Step 1: Understand the configuration
We have two charges, q1=q2=4μC=4×10−6C, placed at points A and B of an equilateral triangle with side length a=0.2m. We need to find the electric potential at point C.
Step 2: Recall the formula for electric potential
The electric potential V due to a point charge q at a distance r is given by:
V=k⋅qr
where k=14πϵ0=9×109N⋅m2C2.
Step 3: Calculate the distance from charges to point C
In an equilateral triangle, the distance from each vertex to the opposite vertex (in this case, from A and B to C) is equal to the side length of the triangle:
- Distance from A to C, r1=0.2m
- Distance from B to C, r2=0.2m
Step 4: Calculate the electric potential at point C
The total electric potential at point C due to both charges is the sum of the potentials due to each charge:
VC=VA+VB
Substituting the values:
VC=k⋅q1r1+k⋅q2r2
Since q1=q2 and r1=r2:
VC=k⋅qr+k⋅qr=2⋅k⋅qr
Step 5: Substitute the known values
Now substituting k=9×109N⋅m2C2, q=4×10−6C, and r=0.2m:
VC=2⋅9×109⋅4×10−60.2
Step 6: Simplify the expression
Calculating the expression:
VC=2⋅9×40.2×103
=2⋅36×103=72×103V
=7.2×104V
Final Result
Thus, the electric potential at point C is:
VC=72,000V or 7.2×104V
We have two charges, q1=q2=4μC=4×10−6C, placed at points A and B of an equilateral triangle with side length a=0.2m. We need to find the electric potential at point C.
The electric potential V due to a point charge q at a distance r is given by:
V=k⋅qr
where k=14πϵ0=9×109N⋅m2C2.
In an equilateral triangle, the distance from each vertex to the opposite vertex (in this case, from A and B to C) is equal to the side length of the triangle:
- Distance from A to C, r1=0.2m
- Distance from B to C, r2=0.2m
The total electric potential at point C due to both charges is the sum of the potentials due to each charge:
VC=VA+VB
Substituting the values:
VC=k⋅q1r1+k⋅q2r2
Since q1=q2 and r1=r2:
VC=k⋅qr+k⋅qr=2⋅k⋅qr
Now substituting k=9×109N⋅m2C2, q=4×10−6C, and r=0.2m:
VC=2⋅9×109⋅4×10−60.2
Calculating the expression:
VC=2⋅9×40.2×103
=2⋅36×103=72×103V
=7.2×104V
Thus, the electric potential at point C is:
VC=72,000V or 7.2×104V
Topper's Solved these Questions
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Relation Between Electric Field And Potential
24 Videos
- ELECTRIC POTENTIAL & CAPACITANCEBOOK - A2ZCHAPTER - ELECTRIC POTENTIAL & CAPACITANCEEXERCISE - Electric Potential Energy
22 Videos
- ELECTRIC CHARGE, FIELD & FLUXBOOK - A2ZCHAPTER - ELECTRIC CHARGE, FIELD & FLUXEXERCISE - Section D - Chapter End Test
29 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - A2ZCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Electric charges q,q,–2q are placed at the corners of an equilateral triangle ABC of side l. The magnitude of electric dipole moment of the system is
View SolutionThree point charges 3nC, 6nC and 6nC are placed at the corners of an equilateral triangle of side 0.1 m. The potential energy of the system is
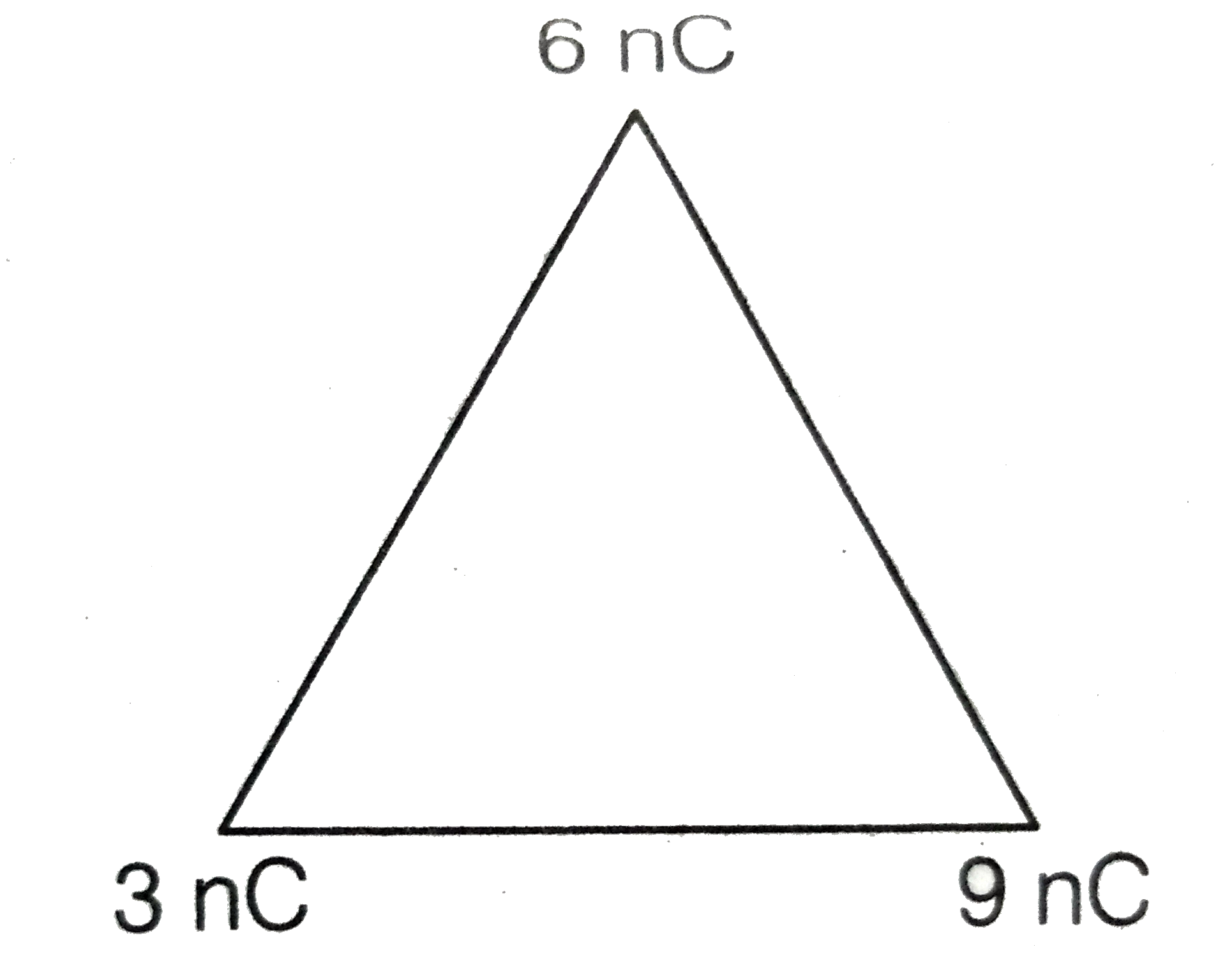
View Solution
Knowledge Check
Three particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
AZeroBInfiniteC27JD100JCharge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
A78 NB39 NC29 ND22.5 NThree charges +Q each are placed at the corners A,B and C of an equilateral triangle. At the circumcenre, O the electric field wil be
 A14pe03Qr2B14pe0Qr2CZeroD14pe0QQr2
A14pe03Qr2B14pe0Qr2CZeroD14pe0QQr2
Charges of +4μC,−6μCand−16μC are placed in air at the corners of an equilateral triangle of side 10. find the potential energy of the system. −0.72J
View SolutionTwo charge +Q each are placed at the two verticles of an equilateral triangle of side a .The intensity of electric field at the third vertex is
View SolutionEqual charges q are placed at the vertices A and B of an equilatral triangle ABC of side a. The magnitude of electric field at the point C is
View SolutionThree charges each20μC are placed at the corners of an equilateral triangle of side 0.4m The potential energy of the system is
View SolutionThree point charges of +2q,+2qand−4q are placed at the corners A, B and C of an equilateral triangle ABC of side x. The magnitude of the electric dipole moment of this system is
View Solution
