Charge of 5μC each are placed at the corners of an equilateral triangle of side 10 cm. Then the force on each charge is :-
78 N
39 N
29 N
22.5 N
The correct Answer is:B
To solve the problem of finding the force on each charge placed at the corners of an equilateral triangle, we can follow these steps:
1. Identify the Charges and Geometry:
- We have three charges Q1,Q2,Q3 each equal to 5μC placed at the corners of an equilateral triangle.
- The side length of the triangle is 10cm=0.1m.
2. Calculate the Force Between Two Charges:
- The force between any two charges can be calculated using Coulomb's Law:
F=14πϵ0|Q1Q2|r2
- Here, ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N⋅m2.
- Substituting the values:
F=14π(8.85×10−12)(5×10−6)2(0.1)2
3. Calculate the Numerical Value of the Force:
- First, calculate (5×10−6)2=25×10−12.
- The distance squared (0.1)2=0.01.
- Now substituting these values into the formula:
F=9×109×25×10−120.01=9×109×2.5×10−10=2.25×10−1N=0.225N
4. Determine the Resultant Force on Each Charge:
- Since the triangle is equilateral, the forces F12 (between Q1 and Q2) and F13 (between Q1 and Q3) will act at an angle of 60∘ to each other.
- The resultant force Fnet can be calculated using the formula:
Fnet=√F212+F213+2F12F13cos(60∘)
- Since F12=F13=F:
Fnet=√F2+F2+2F2⋅12=√3F2=F√3
- Substituting the value of F:
Fnet=0.225√3≈0.225×1.732≈0.389N
5. Final Result:
- The force on each charge is approximately 0.389N.
- We have three charges Q1,Q2,Q3 each equal to 5μC placed at the corners of an equilateral triangle.
- The side length of the triangle is 10cm=0.1m.
- The force between any two charges can be calculated using Coulomb's Law:
F=14πϵ0|Q1Q2|r2
- Here, ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N⋅m2.
- Substituting the values:
F=14π(8.85×10−12)(5×10−6)2(0.1)2
- First, calculate (5×10−6)2=25×10−12.
- The distance squared (0.1)2=0.01.
- Now substituting these values into the formula:
F=9×109×25×10−120.01=9×109×2.5×10−10=2.25×10−1N=0.225N
- Since the triangle is equilateral, the forces F12 (between Q1 and Q2) and F13 (between Q1 and Q3) will act at an angle of 60∘ to each other.
- The resultant force Fnet can be calculated using the formula:
Fnet=√F212+F213+2F12F13cos(60∘)
- Since F12=F13=F:
Fnet=√F2+F2+2F2⋅12=√3F2=F√3
- Substituting the value of F:
Fnet=0.225√3≈0.225×1.732≈0.389N
- The force on each charge is approximately 0.389N.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise -3 Section (B) Previous Year Problems | JEE Main
30 Videos
- ELECTROSTATICSBOOK - MOTIONCHAPTER - ELECTROSTATICSEXERCISE - Exercise - 2 (Objective Problems | NEET)
64 Videos
- ELECTRONICS - SEMI CONDUCTORBOOK - MOTIONCHAPTER - ELECTRONICS - SEMI CONDUCTOREXERCISE - EXERCISE - 3
29 Videos
- ELECTROSTATICS - I BOOK - MOTIONCHAPTER - ELECTROSTATICS - I EXERCISE - EXERCISE - 4 (Level -II) PREVIOUS YEAR - JEE ADVANCED
13 Videos
Similar Questions
Three points charges of 1C,2Cand3C are placed at the corners of an equilateral triangle of side 100 cm. Find the work done to move these charges to the corners of a similar equilateral triangle of side 50 cm.
View SolutionThree particles have charges +10μ C each and they are fixed at the corners of an equilateral triangle of side 0.5m .The force on each of the particles has magnitude:
View Solution
Knowledge Check
Three particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
AZeroBInfiniteC27JD100J3 particles of mass 10 gm each are placed at the corners of an equilateral triangle of side 5 cm. The M.I. of the system about a perpendicular axis to the plane passing through a corner of the triangle will be : (in kg-m2)
A5×10−2B5×10−3C5×10−4D5×10−5Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
Ama2B3ma2C34ma2D23ma2
Three points charges are placed at the corners of an equilateral triangle of side L as shown in the figure:
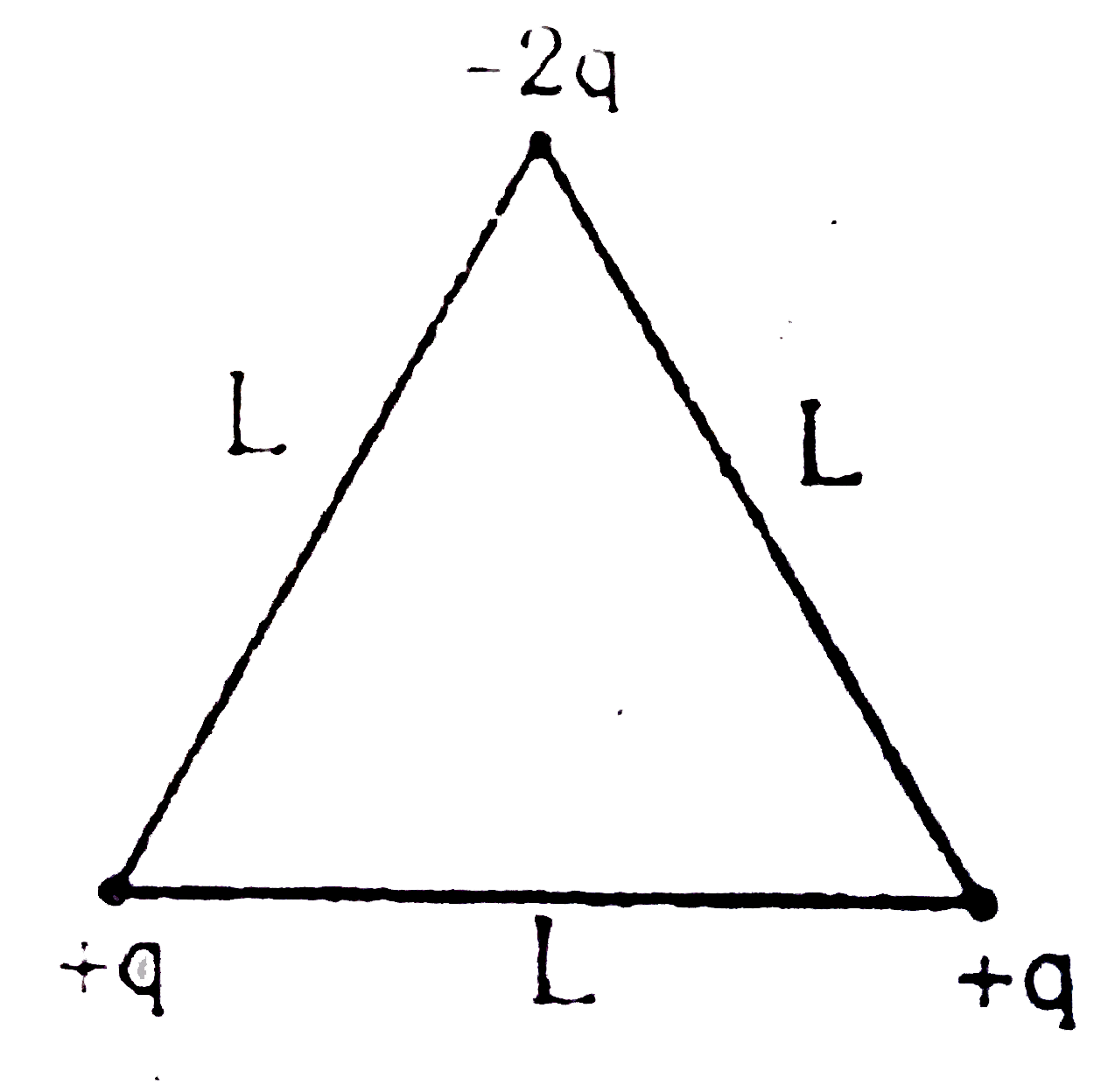
View SolutionConsider the charges q,q and -q placed at the vertices of an equilateral triangle of each side l. What is the force on each charge ?
View SolutionThree point charges 2μC,3μCand5μC are placed at the corners of an equilateral triangle of side 200 cm. Calculate the potentail energy of the system.
View SolutionA charge of 0.5 nC is placed at the centre of an equilateral triangle of side 10 cm, calculate the work done in bringing a charge of 0.1 nC from infinity to any vertices of the triangle.
View SolutionEqual charges of +4μC are placed at the three corners of an equilateral triangle of side 2m. Calculate the magnitude and direction of the force on one of the charges.
View Solution