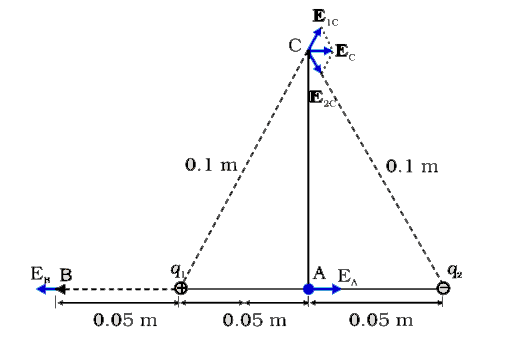
Two point charges $q_{1} and q_{2}$ , of magnitude $+ 10^{- 8} C and - 10^{- 8} C$ , respectively, are placed 0.1 m apart. Calculate the electric fields at points A, B and C shown in Fig. 1.14.

A

$E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the RIGHT.

B

$E_{A} = 7.2 \times 10^{- 4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the left.

C

$E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the left.

D

$E_{A} = 7.2 \times 10^{4} N C^{- 1}$ $E_{B} = 3.2 \times 10^{- 4} N C^{- 1}$
$E_{B}$ is directed towards the left.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

The electric field vector E1A at A due to the positive charge q1 points towards the right and has a magnitude
$E_{1 A} = \frac{(9 \times 10^{9} N m C^{2}) \times (10^{- 8} C)}{(0.05 m^{2})} = 3.6 10^{4} N C^{- 1}$
The electric field vector E2A at A due to the negative charge q2 points towards the right and has the same magnitude. Hence the magnitude of the total electric field EA at A is
$E_{A} = E_{1 A} + E_{2 A} = 7.2 \times 10^{4} N C^{- 1}$
$E_{A}$ is directed toward the light.
The electric field vector E1B at B due to the positive charge q1 points towards the left and has a magnitude
$E_{1 B} = \frac{(9 \times 10^{9} N m^{2} C^{- 2}) \times (10^{- 8 C})}{{(0.05 m)}^{2}} = 3.6 \times 10^{4} N C^{- 1}$
The electric field vector E2B at B due to the negative charge q2 points towards the right and has a magnitude
$E_{1 B} = \frac{(9 \times 10^{9} N m^{2} C^{- 2}) \times (10^{- 8 C})}{{(0.15 m)}^{2}} = 4 \times 10^{3} N C^{- 1}$
The magnitude of the total electric field at B is
$E_{B} = E_{1 B} - E_{2 B} = 3.2 \times 10^{4} N C^{- 1}$
$E_{B}$ is directed towards the left.
The directions in which these two vectors point are indicated in Fig. 1.14. The resultant of these two vectors is
$E_{C} = E_{1} \frac{cos (π)}{3} + E_{2} Cos \frac{π}{3} = 9 \times 10^{- 3} N C^{- 1}$
$E_{c}$ points towards the right.

Updated on:21/07/2023

|

Class 12 PHYSICS ELECTROSTATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two point charges $+ 10^{- 7} C$ and $- 10^{- 7} C$ are placed at A and B 20 cm apart as shown in the figure. Calculate the electric field at C, 20 cm apart from both A and B.

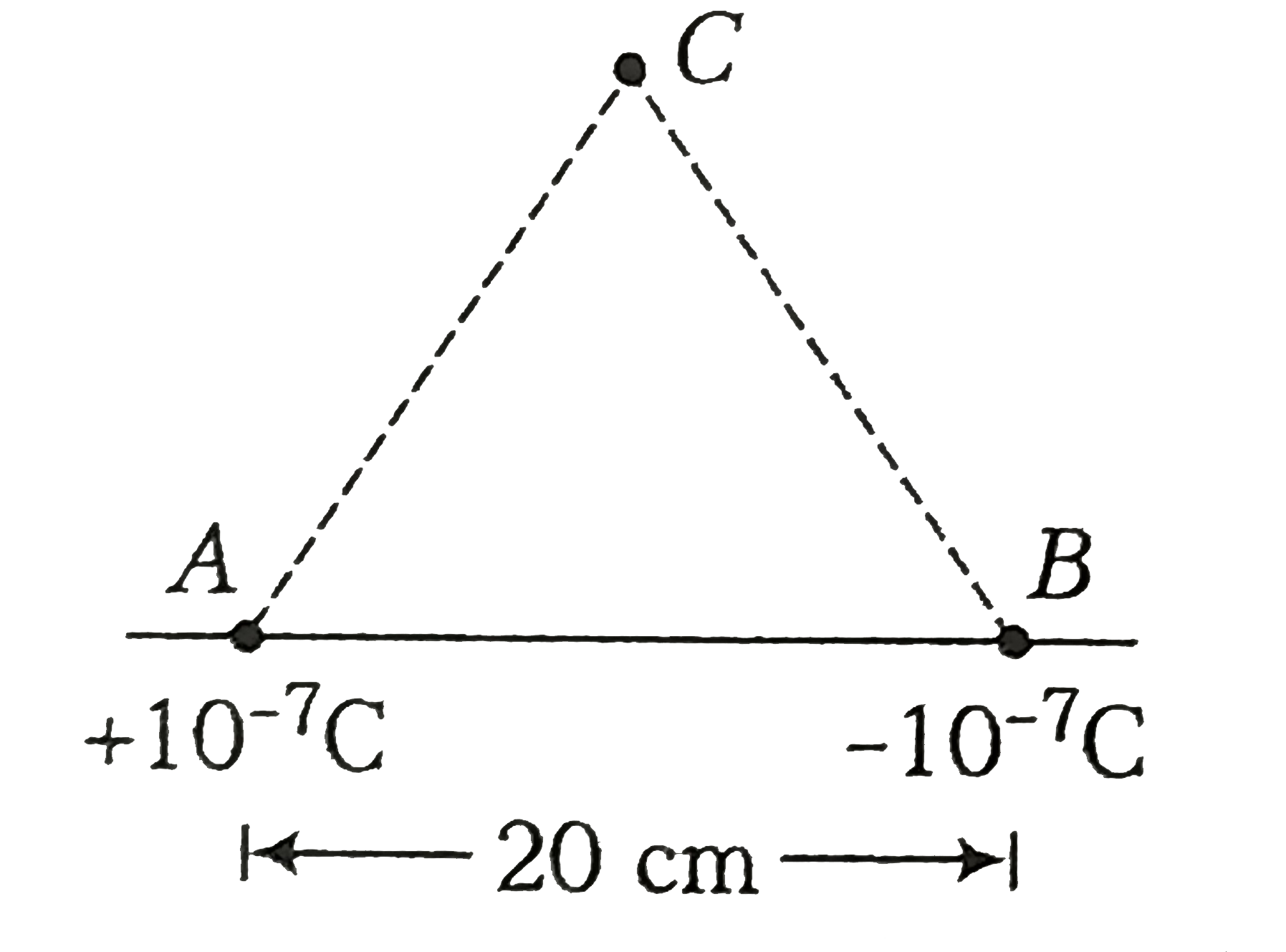A $1.5 \times 10^{- 5} N C^{- 1}$
B $2.2 \times 10^{4} N C^{- 1}$
C $3.5 \times 10^{6} N C^{- 1}$
D $3.0 \times 10^{5} N C^{- 1}$
In, the charges on $C_{1}, C_{2}$ , and $C_{3}$ , are $Q_{1}, Q_{2}$ , and $Q_{3}$ , respectively.
.
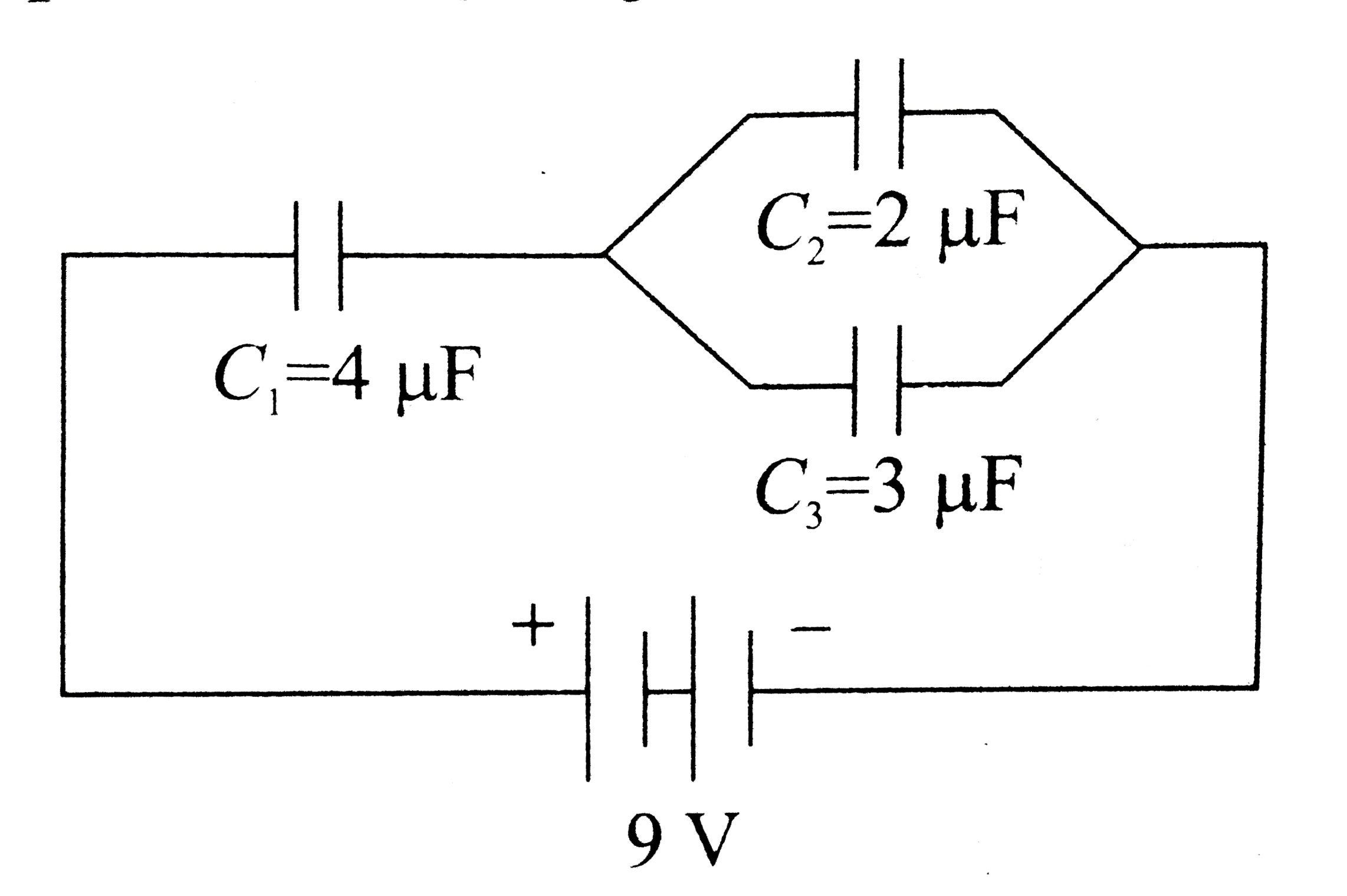A $Q_{2} = 8 μ C$
B $Q_{3} = 12 μ C$
C $Q_{1} = 20 μ C$
D $Q_{2} = 12 μ C$

NCERT-ELECTRIC CHARGES AND FIELDS-EXERCISE

Home
Ask Doubt
Profile