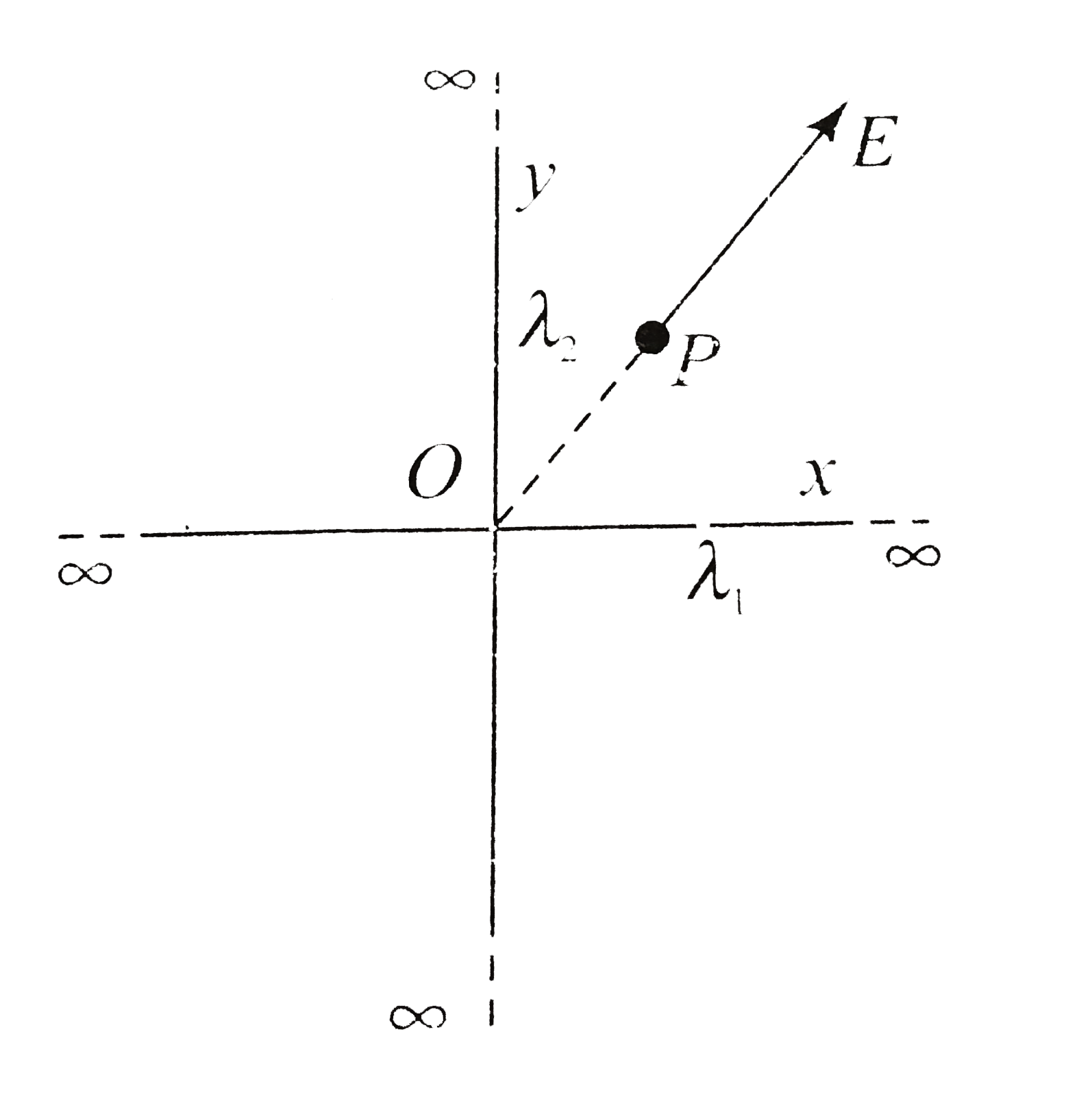
Two mutually perpendicular infinite wires along x-axis and y-axis carry charge densities $λ_{1} and λ_{2}$ . The electric line of force at P is along the line $y = x / (\sqrt{3})$ , where P is also a point lying on the same line. Find $λ_{2} / λ_{1}$ .

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Net electric field is $¯ p, \to E = {\to E}_{1} + {\to E}_{2}$ due to vertical wire
${\to E}_{2} = \frac{λ_{2}}{2 π e_{0} x}$ due to vertical wire in x-direction, a angle of electric field with x direction
$tan a = \frac{E_{1}}{E_{2}} = \frac{λ_{1} / 2 π e_{0} y}{λ_{2} / 2 π e_{0} x} or \frac{1}{\sqrt{3}} = \frac{λ_{1} x}{λ_{2} y} or \frac{λ_{2}}{λ_{1}} = \frac{x}{y} \sqrt{3} or \frac{λ_{2}}{λ_{1}} = 3$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
Two mutually perpendicular wire carry charge densities $λ_{1} and λ_{2}$ . The electric lines of force makes angle $α$ with second wire, then $λ_{1} / λ_{2}$ is

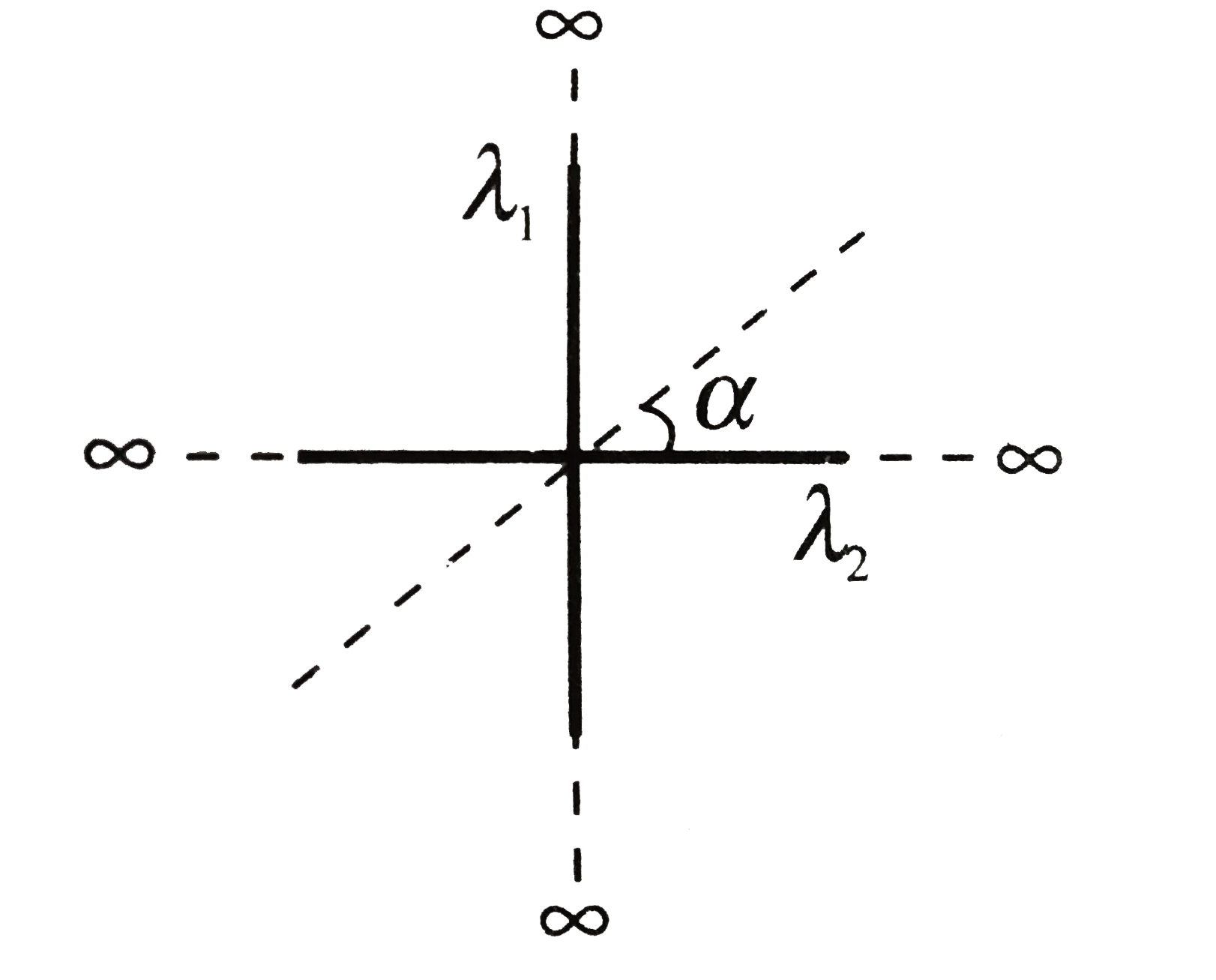A ${tan}^{2} α$
B ${cot}^{2} α$
C ${sin}^{2} α$
D ${cos}^{2} α$
Question 2 - Select One
For an infinite line of charge having linear charge density $λ$ lying along x-axis the work done in moving a charge $q$ form $C$ to $A$ along $C A$ is

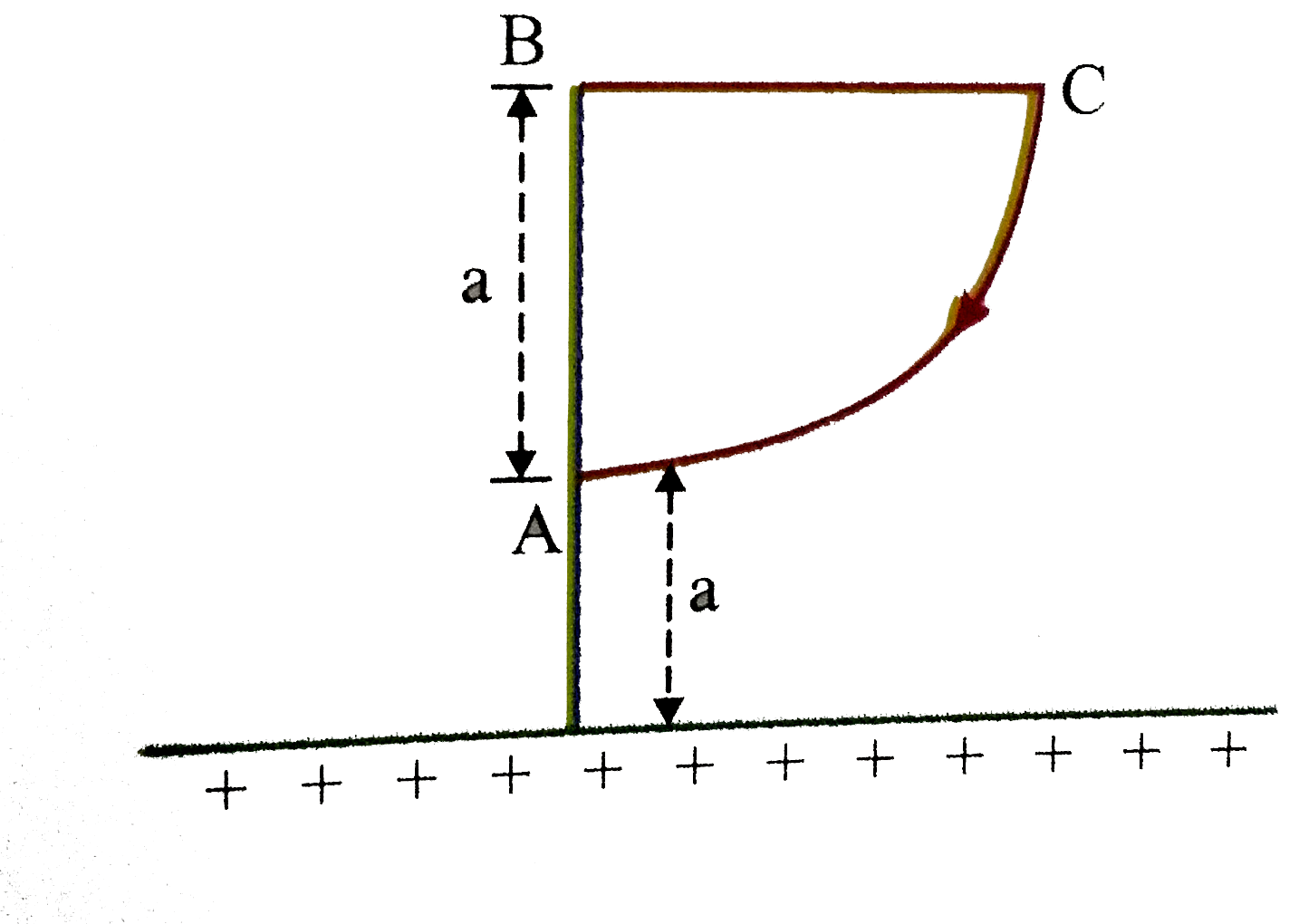A $\frac{q λ}{2 π ε_{0}} In 2$
B $\frac{q λ}{2 π ε_{0}} In \sqrt{2}$
C $\frac{q λ}{4 π ε_{0}} In 2$
D $\frac{q λ}{2 π ε_{0}} In (0.5)$
Question 3 - Select One
Two uniformly long charged wires with linear densities $λ$ and $3 λ$ are placed along X and Y axis respectively. Determined the slope of electric field at any point on the l ine $y = \sqrt{3} x$
A $3 \sqrt{3}$
B $\frac{\sqrt{3}}{3 \sqrt{2}}$
C $\frac{1}{3 \sqrt{3}}$
D $\sqrt{3}$

Recommended Questions

Home
Ask Doubt
Profile