Two point charges Q1 and Q2 are positioned at points I and 2. The field intensity to the right of the charge Q2 on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l.
![Two point charges Q(1) and Q(2) are positioned at points I and 2. The field intensity to the right of the charge Q(2) on the line that passes through the two charges varies according to a law that is represented in the figure. The field intensity is assumed to be positive if its direction coincides with the positive direction on the x-axis. The distance between the charges is l. (a) Find the sign of each charge (b) Find the ratio of the absolute values of the charges |(Q(1))/(Q(2))| (c) Find the value of b where the field intensity is maximum [(a) Q(2) is negative and Q(1) is positive (b) ((l +a)/(a))^(2), (c) (l)/(((l+a)/(a))^(2//3)-1)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/GAL_PHY_V03A_ECA_C01_E01_130_Q01.png)
(a) Find the sign of each charge
(b) Find the ratio of the absolute values of the charges ∣∣∣Q1Q2∣∣∣
(c) Find the value of b where the field intensity is maximum
[(a) Q2 is negative and Q1 is positive (b) (l+aa)2, (c) l(l+aa)2/3−1⎤⎥
⎥
⎥⎦
1Q1/Q1/32+1
1Q1/Q1/32−1
1Q1/Q1/31+1
1Q2/Q1/31+1
The correct Answer is:B
Electric field at any position to the right of charges
E=E1−E2=14πe0Q1(1+x)2−14πe0Q2x2
For maximum value of E
dEdx=0⇒ddx[14πe0Q1(1+x)2−14πe0Q2x2]=0,Q1=−2(1+x)3−Q2−2x3=0
Q1(1+x)3=Q2x3⇒(1+xx)3=Q1Q2,1+xx=(Q1Q2)1/3⇒1x=(Q1Q2)1/3−1,x=1(Q1Q2)1/3−1
Similar Questions
Two point charge Qa and Qb are positional at point A and B. The field strenght to the right of charge Qb on the line that passes therough the two charges varies according to a law represented schematically in fig. (without employing a definite scale). The field strength is assumed to be positive if its direction coincedes with the positive direction of the x-axis. The distance between the charges is l=21cm.
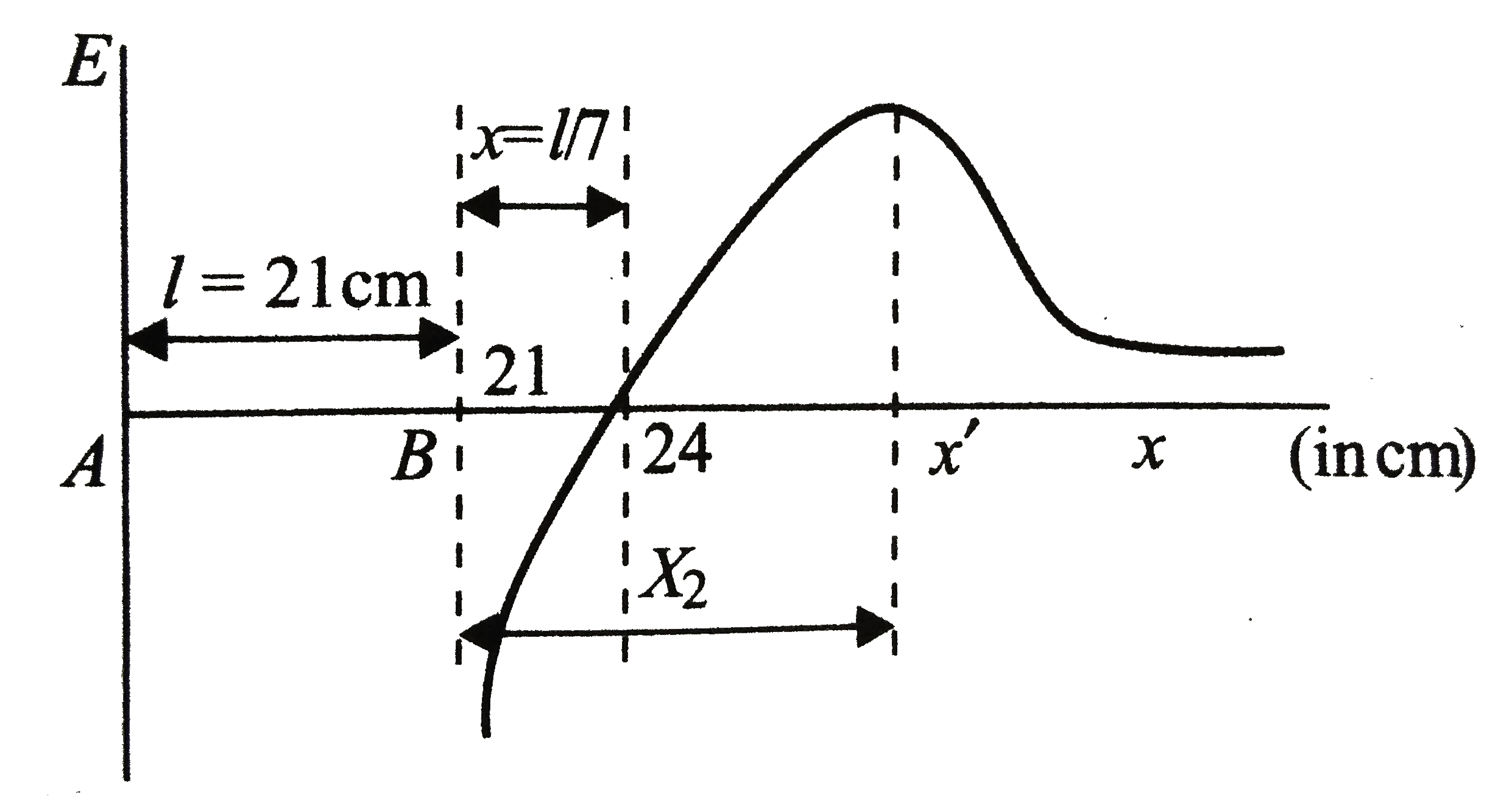
(a) Find the sign of the charges.
(b) Find the ration between the absolute value of charge Qa and Qb.
(c ) Find the coordinate x of the point where the field strenght is maximum.
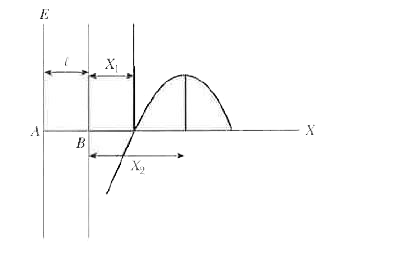
View SolutionTwo points like charges QA and QB are positioned at points a and B (see figure). The electric field strength to the right of charge QB on the line that passes through the two charges varies according to a law that is represented schematically in Figure below accompaanying the problem without employing a definite scale. Assume electric field to be positive if its direct ion coincides with (the positive direction on the x-axis. THe distance between the charges is l.

View Solution
Knowledge Check
Charges +2Q and −Q are placed as shown in figure. The point at which electric field intensity is zero will be
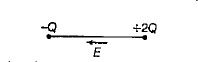 ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2Q
ASomewhere between −Q and +20BSomewhere on the left of −QCSomewhere on the right of +2QDSomewhere on the right bisector of line Joining−Q and +2QThe positions of two point charges q1 and q2 are →r1 and →r2 , respectively. Find the position of the point where the net field is zero due to thses charges.
A→r1√q1+→r2√q2√q1+√q2B→r1√q2+→r2√q1√q1+√q2C→r1√q2+→r2√q1√q1+q2D→r1√q1+→r2√q2√q1+q2Two point charges(+Q) and (−2Q) are fixed on the X-axis at position a and 2a from origin respectively. At what position on the axis, the resultant electric field is zero
AOnly x=√2aBOnly x=−√2aCBoth x=±√2aDx=3a2cm
Two point charges q1andq2 are kept r distance apart in a uniform external electric field →E. Find the amount of work done in assembling this system of charges.
View SolutionTwo point-like charges a and b whose strengths are equal in absolute value are positioned at a certain distance from each other. Assuming the field strength is positive in the direction coinciding with the positive direction of the r axis, determine the signs of the charges for each distribution of the field strength between the charges shown in Figures (a),(b),(c),and(d).
View SolutionTwo point charges+ q and-q are placed at distanced apart. What are the points at which the resultant field is parallel to the line joining the two charges ?
View SolutionA positive charge +q1 is located to the left of a negative charge −q2 On a line passing through the two charges, there are two places where the total potential is zero. The reference is assumed to be at infinity The first place is between the charges and is 4.00 cm to the left of the negative charge. The second place is 7.00cm to the right of the negative charge if q2=−12μC , what is the value of charge q1∈μC
View SolutionTwo point charges(+Q) and (−2Q) are fixed on the X-axis at position a and 2a from origin respectively. At what position on the axis, the resultant electric field is zero
View Solution