A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is 1.0 meter above the ground level and the top of the track is 2.4 meter above the ground. Find the distance on the ground with respect to a point B( which is vetically below the end A of the track as shown in fig.) where the sphere lands.
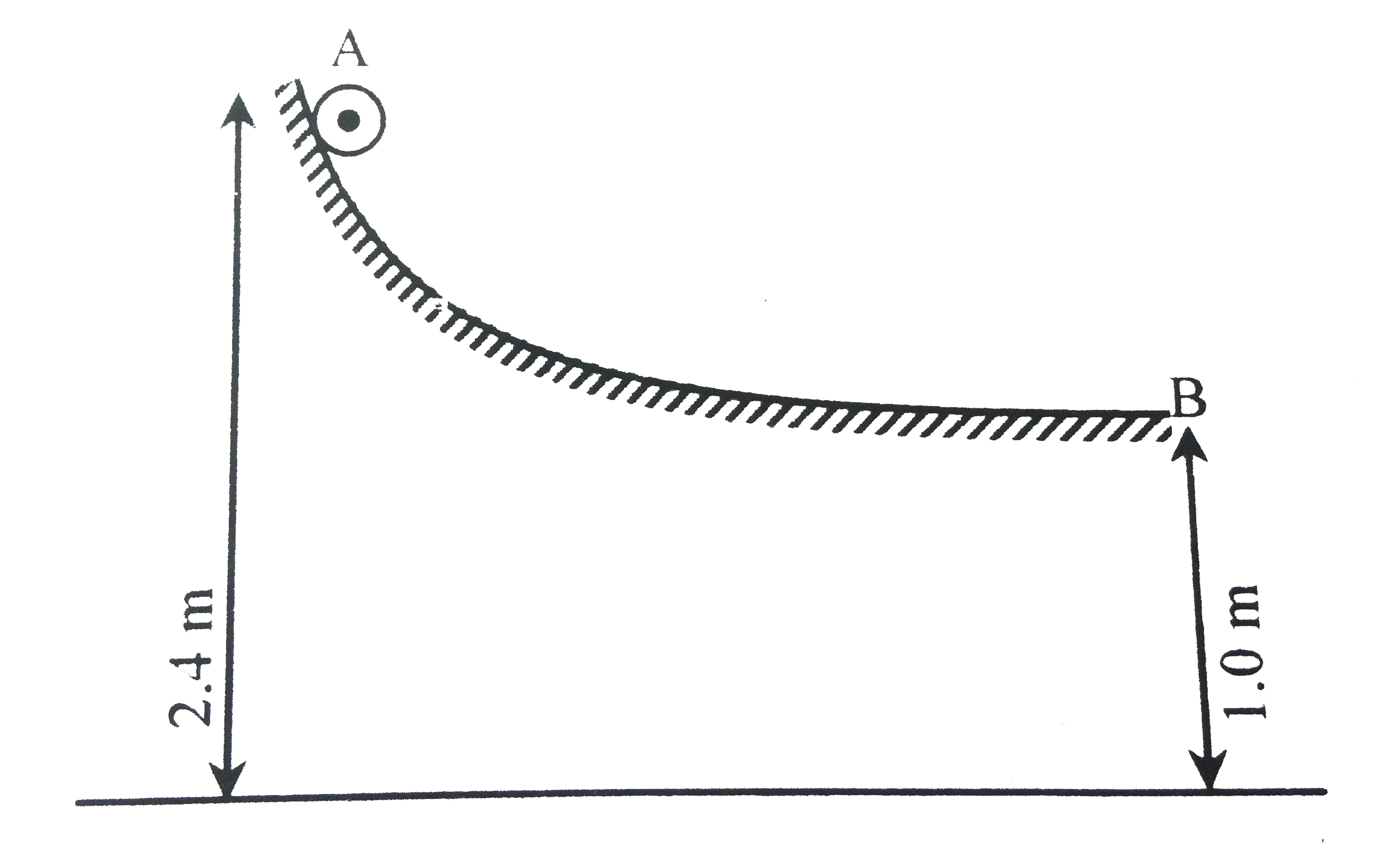 .
.
(A) 1m
(B) 2m
( C) 3m
(D) 4m.
The correct Answer is:B
Applying law of conservation of mechanical energy at point M and point N ΔK+ΔU=0

Increases in KE = Decreases in PE
(12mv2+12Iω2−0)=(mg(2A)−mg(L))
Since, the sphere is of rolling without slipping
u=rω hence, ω=ur
Where r is the radius of the sphere
Also, I=25mr2,∴12mv2+12×25mr2×v2r2=mg(2A)−mg(l)
⇒v=4.43m/s
After point N, the sphere takes a parabolic path. Considering the motion of sphere in vertical direction.
uy=0,sy=1m,ay=9.8m/s2
Using sY=uyt+12ayt2,1=4.9t2⇒t=1√4.9=0.45 sec.
In horizontal direction, the velocity of sphere remains constant,
Hence, =v×t=4.43×0.45=2m.
Similar Questions
A small sphere rolls from the top of a sloping curved plane without slipping. The end of the plane is horizontal which is 1.0 m above the ground level and the top of the plane is 2.6 m above the ground. With respect to the point B on the ground (which is just below the point A at the end of the plane), find the distance where the sphere falls. Does the sphere continue to rotate about its center of mass during the projectile motion? explain.
View SolutionA small spherical ball is released from a point at a height h on a rough track shown in figure. Assuming that it does not slip anywhere, find its linear speed when it rolls on the horizontal part of the track.

View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 , above the horizontal surface, the distance it will move on the rough surface is x meter. Then value of x.

View SolutionFrom a point on the level ground , the angel of elevation of the top of a pole is 30∘. On moving 20 meters nearer, the angle of elevation is 45∘. Then the height of the pole, in meters, is
View SolutionThe elevation of top of a hill is observed from a certain point in the horizontal plane through its base, to be 30∘. After walking 120 meters towards it on level ground the elevation is found to be 60∘. Then the height of the object (in meters) is
View SolutionA solid cylinder of mass M and radius R rolls down an inclined plane of height h without slipping. The speed of its centre when it reaches the bottom is.
View Solution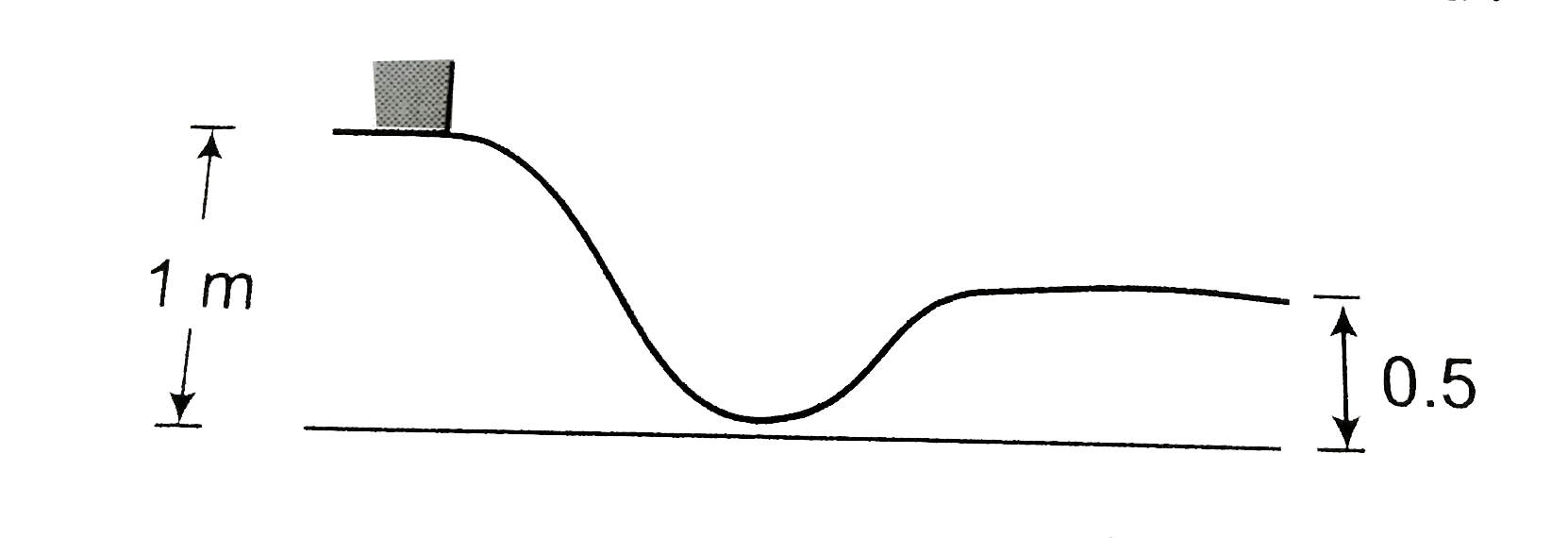
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View Solution
The figure shown a particle sliding on a frictionless track, which teminates in a straight horizontal section. If the particle starts slipping from the point A, how far away from the track will the particle hit the ground?
View Solution