Question

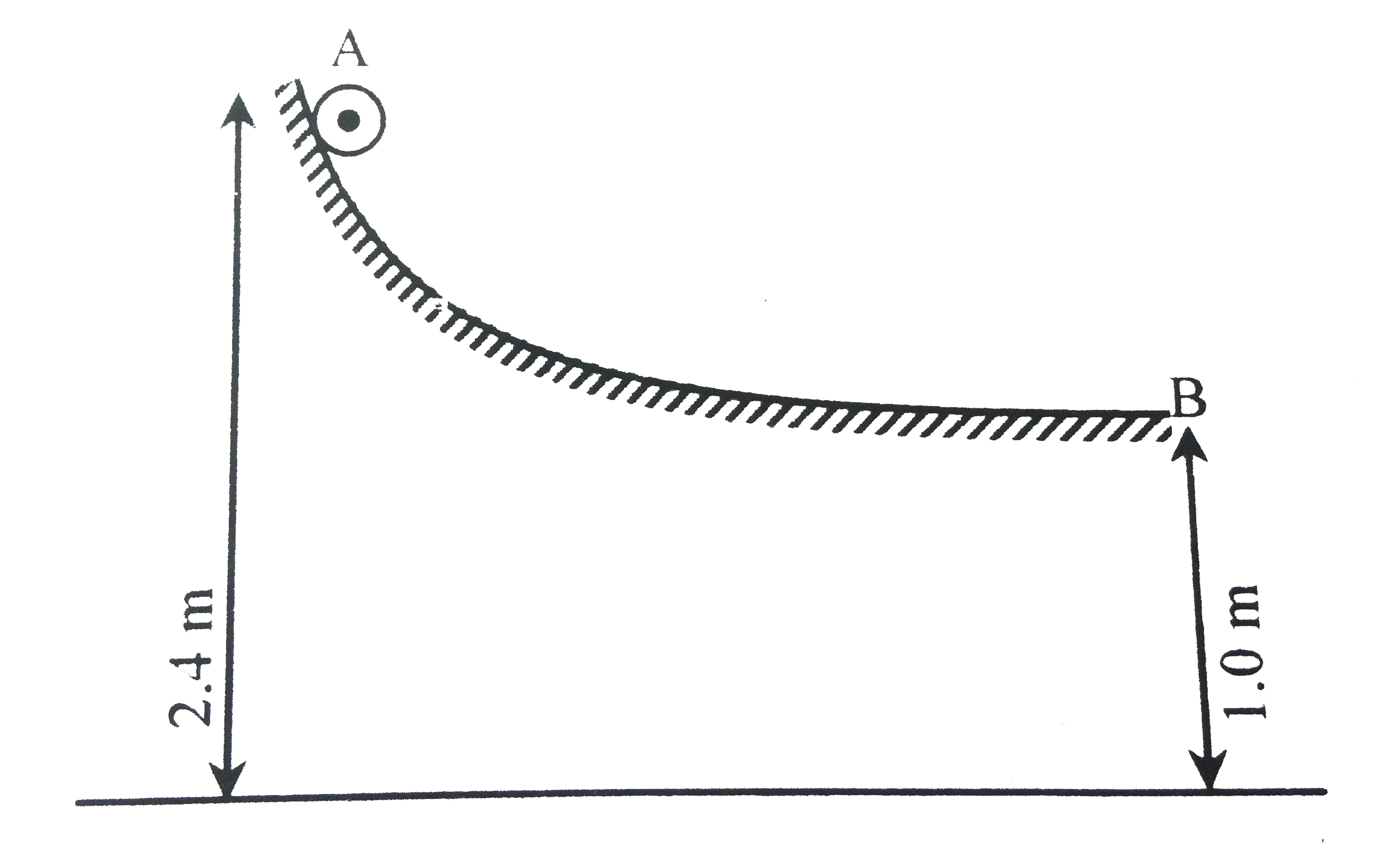
A small sphere rolls down without slipping from the top of a track in a vertical plane. The track has an elevated section and a horizontal part. The horizontall part is $1.0$ meter above the ground level and the top of the track is $2.4$ meter above the ground. Find the distance on the ground with respect to a point $B$( which is vetically below the end $A$ of the track as shown in fig.) where the sphere lands.
.
(A) $1m$
(B) $2m$
( C) $3m$
(D) $4m$.

Explanation

`(B)` Let `m` be the mass and `r` the radius of the sphere. Let `v` and `omega` be the linear and angular velocities at `A`. In rolling down from the top of the track to the point `A` the sphere loses potential energy which appears as linear and rotational kinetic energies in the sphere. Thus
`m g h = (1)/(2) mv^(2) + I omega^(2)`
But `I = (2)/(5) mr^(2)` and `omega = (v)/( r)`
`m g h = (1)/(2) mv^(2) + (1)/(2) ((2)/(5) mr^(2)) (v^(2))/(r^(2))`
`m g h = (1)/(2) mv^(2)`
or `v^(2) = (10)/(7) g h`,
Here `h - (2.4 - 1.0) = 1.4 meter`
`v =sqrt(((10)/(7) gh)) = sqrt(((10g(1.4))/(7))) = sqrt(2 g)`
`v` is the horizontal velocity of the sphere at `A`. The vertical velocity at `A` is zero. If `t` is the time taken in covering the vertical distance `AB (=1.0 m)`, then using the formula `h = 1//2 gt^(2)`, we have.
`rArr t = sqrt(((2h)/(g))) = sqrt(((2)/(g))) (because h = 1.0 m)`
The horizontal distance moved in time `t = v xx t`
=` sqrt(2 g) xx sqrt(((2)/(g))) = 2 m`
During the flight the sphere continues to rotate about its centre of mass due to conservations of angular momentum.