A thin and uniform rod of mass M and length L is held vertical on a floor with large friction. The rod is released from rest so that it falls by rotating about its contact-point with the floor without slipping. Which of the following statement(s) is(are) correct, when the rod makes an angle 60° with vertical? [g is the acceleration due to gravity]
The normal reaction force from the floor on the rod will be Mg16
The angular acceleration of the rod will be 2gL
The radial acceleration of the rod’s center of mass will be 3g4
The angular speed of the rod will be √3g2L
The correct Answer is:A, C, D

Loss in GPE = gain in KE
mg×[l2−l4]=12×ml23×ω2
mg×l4=12ml23×ω2⇒ω=√3g2l
τp=IP×α⇒mg×la×√32=ml23×α⇒α=3√3g4l
aR=ω2l2=3g2l×l2=3g4
Mg−N=MACM'Y=M(ω2l2cos60∘+αl2cos30∘)
Mg−N=M[3g8+3√38×g×√32]
Mg[38+916]=15Mg16⇒N=Mg16
Correct options are (A), ( C), (D)

Similar Questions
A uniform rod of mass M and length L is hinged at its end. The rod is released from its vertical position by slightly pushing it. What is the reaction at the hinge when the rod becomes horizontal, again vertical.
View SolutionA rod of mass m and length l is held vertically on a smooth horizontal floor. Now it is released from this position, find the speed of its centre of mass when it makes an angle θ with the vertical.
View Solution
Knowledge Check
A thin and uniform rod of mass M and length L is held vertical on floor with large friction. The rod is released from rest so that is falls by rotating about is contact-point with the floor without slipping. Which of the following statement(s) si/are correct. When the rod makes an angle 60∘ with vertical? [g is the acceleration due to gravity]
AThe Normal reaction force from the floor on the rod will be Mg16BThe angular acceleration of the rod will be 2gLCThe angular speed of the rod will be √3g2LDThe radial acceleration of the rod's center of mass will be 3g4A thin uniform rod mass M and length L is hinged at its upper end. And released from rest from a horizontal position. The tenstion at a point located at a distance L/3 from the hinge point, when the rod become vertical will
A22Mg/27B11Mg/13C6Mg/11D2Mg
A uniform rod of mass M and length L is free to rotate about a frictionless pivot located L/3 from one end. The rod is released from rest incrementally away from being perfectly vertical, resulting in the rod rotating clockwise about the pivot. when the rod is horzontal what is the magnitude of the tangential acceleration of its center of mass?Ag/6Bg/2Cg/4D2g/3
A thin uniform rod AB of mass m and length l is hinged at one end to the level floor and stands vertically. If it s allowed to fall, with what angular velocity will it strike the floor?
View SolutionA rod of mass m and length l is himged about one of its ends. The rod is released from horizontal position. When the rod becomes vertical, calculate (i) angular speed of the rod (ii) Hinge reaction.
View SolutionA thin uniform rod of mass m and length l is free to rotate about its upper end. When it is at rest, it receives an impulse J at its lowest point, normal to its length immediately after impact,
View SolutionA thin uniform rod of mass m and length l is free to rotate about its upper end. When it is at rest, it receives an impulse J at its lowest point, normal to its length. Immediately after impact,
View SolutionA slender uniform rod of mass M and length l is pivoted at one ens so that it can rotate in a vertical plane, Fig. There is negligible friction at the pivot. The free end is held vertically above the pivot and then released. The angular acceleration of the rod when it makes an angle θ with the vertical is
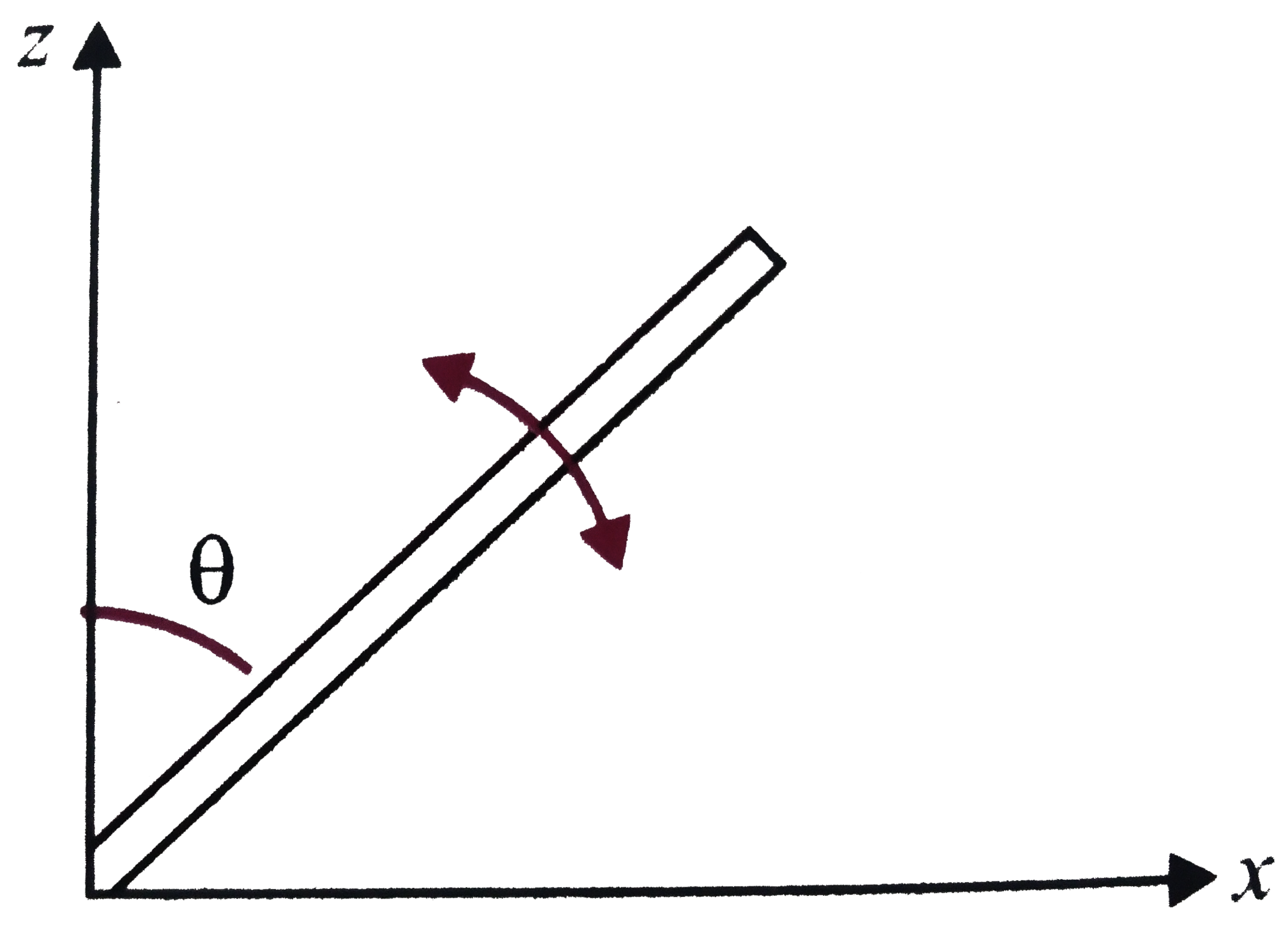
View Solution
