Determine the minimum coefficient of friction between a thin rod and a floor at which a person can slowly lift the rod from the floor, without slipping, to the vertical position applying at its end a force always perpendicular to its length.
The correct Answer is:12√2
Consider a general position of the rod as shown in the figure. Let the applied force be F. As the end is moved slowly, some rod has no acceleration. Applying Newton's law in x-direction, f−Fsinθ=0

f=Fsinθ
In y-direction Fcosθ+n=mg ......iii
Making τA=0⇒Fl−mg12cosθ=0
F=mgcosθ2.........iii
For no slipping f≤μN⇒μ≥fN
μ≥Fsinθmg−fcosθ⇒μ≥sinθcosθ2−cos2θ
μmin=(sinθcosθ2−cos2θ)=12√2
Topper's Solved these Questions
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Single Correct
Explore 142 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Multiple Correct
Explore 26 Videos
- RIGID BODY DYNAMICS 2Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 2Exercise:Exercise 3.4
Explore 13 Videos
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICSChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
- SOUND WAVES AND DOPPLER EFFECTBook:CENGAGE PHYSICSChapter:SOUND WAVES AND DOPPLER EFFECTExercise:Integer
Explore 16 Videos
Similar Questions
Determine the minimum coefficient of friction μmin between a thin homogeneous rod and a floor at which a person can slowly lift the rod from the floor without slippage to the vertical position, applying to its end a force perpendicualr to it.
View SolutionA block of mass m slips on a rough horizontal table under the action of horiozontal force applied to it. The coefficient of friction between the block and the table is μ. The table does not move on the floor. Find the total frictional force aplied by the floor on the legs of the table. Do you need the friction coefficient between the table and the floor or the mass of the table ?
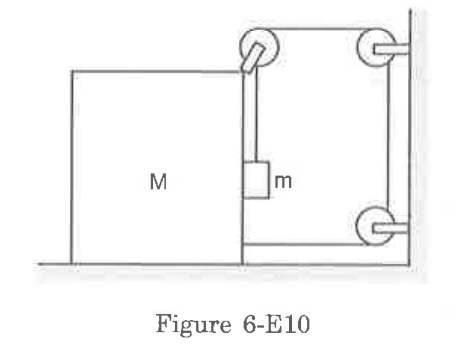
View Solution
Knowledge Check
The moment of inertia of thin rod of linear density λ and length l about an axis passing through one end and perpendicular to its length is
Aλl212Bλl23Cλl312Dλl33Consider a thin uniform rod having length 'L' and mass 'M'. Its moment of inertia about an axis passing through mid-point between centre point and one end and perpendicular to its length is
A7ML248B7ML236C7ML224D7ML212The moment of inertia of a thin uniform rod of mass M and length L about an axis perpendicular to the rod, through its centre is I. The moment of inertia of the rod about an axis perpendicular to rod through its end point is
AI4BI2C2ID4I
The friction coefficient between the board and the floor shown in figure is μ Find the maximum force that the man can exert on the rope so that the board does not slip on the floor

View SolutionA uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform beam of mass m is inclined at an angle θ to the horizontal. Its upper end produces a ninety degree bend in a very rough rope tied to a wall, and its lower end rests on a rough floor (a) If the coefficient of static friction between beam and floor is μs determine an expression for the maximum mass M that can be suspended from the top before the beam slips. (b) Determine the magnitude of the reaction force at the floor and the magnitude of the force exerted by the beam on the rope at P in terms of m,M and μs
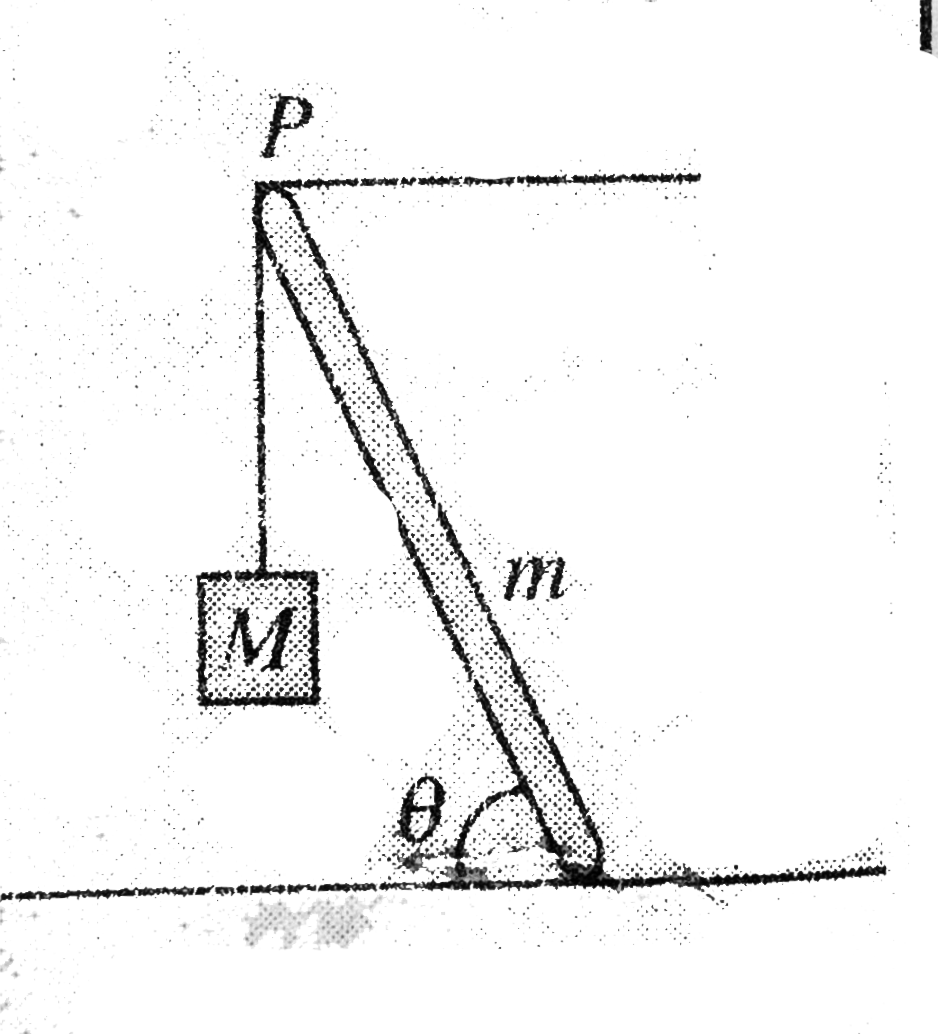 .
.
View SolutionM.I. of a thin uniform rod about the axis passing through its centre and perpendicular to its length is ML2/12 . The rod is cut transversely into two halves, which are then riveted end to end.M.I. of the composite rod about the axis passing through its centre and perpendicular to its length will be
View SolutionA thin rod of length L is vertically straight on horizontal floor. This rod falls freely to one side without slipping of its bottom. The linear velocity of centre of rod when its top end touches floor is
View Solution

