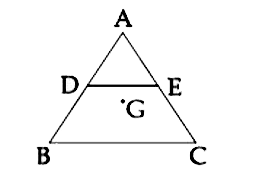
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is $I_{0}$ If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

$I = \frac{9}{16} I_{0}$

$I = \frac{15}{16} I_{0}$

$I = \frac{3}{4} I_{0}$

$I = \frac{I_{0}}{4}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

D,E and F are the middle points of the sides of the triangle ABC, then
Acentroid of the triangle DEF is the same as that of ABC
Borthocentre of the traiangl DRF is the circumcentre of ABC
Corthocentre of the triangle DEF is the incentre of ABC
Dcentroid of the triangle DEF is not the same as that of ABC
Three point masses each of mass m are placed at the corners of an equilateral triangle of side 'a'. Then the moment of inertia of this system about an axis passing along one side of the triangle is
A $m a^{2}$
B $3 m a^{2}$
C $\frac{3}{4} m a^{2}$
D $\frac{2}{3} m a^{2}$
Three particles each of 'm' are kept at the three vertices of an equilateral triangle of side 'a' . Moment of inertia of the system about an axis passing through the centroid and perpendicular to its plane is
A $3 m a^{2}$
B $m a^{2}$
C $m a^{2} / 3$
D $2 / 3 m a^{2}$