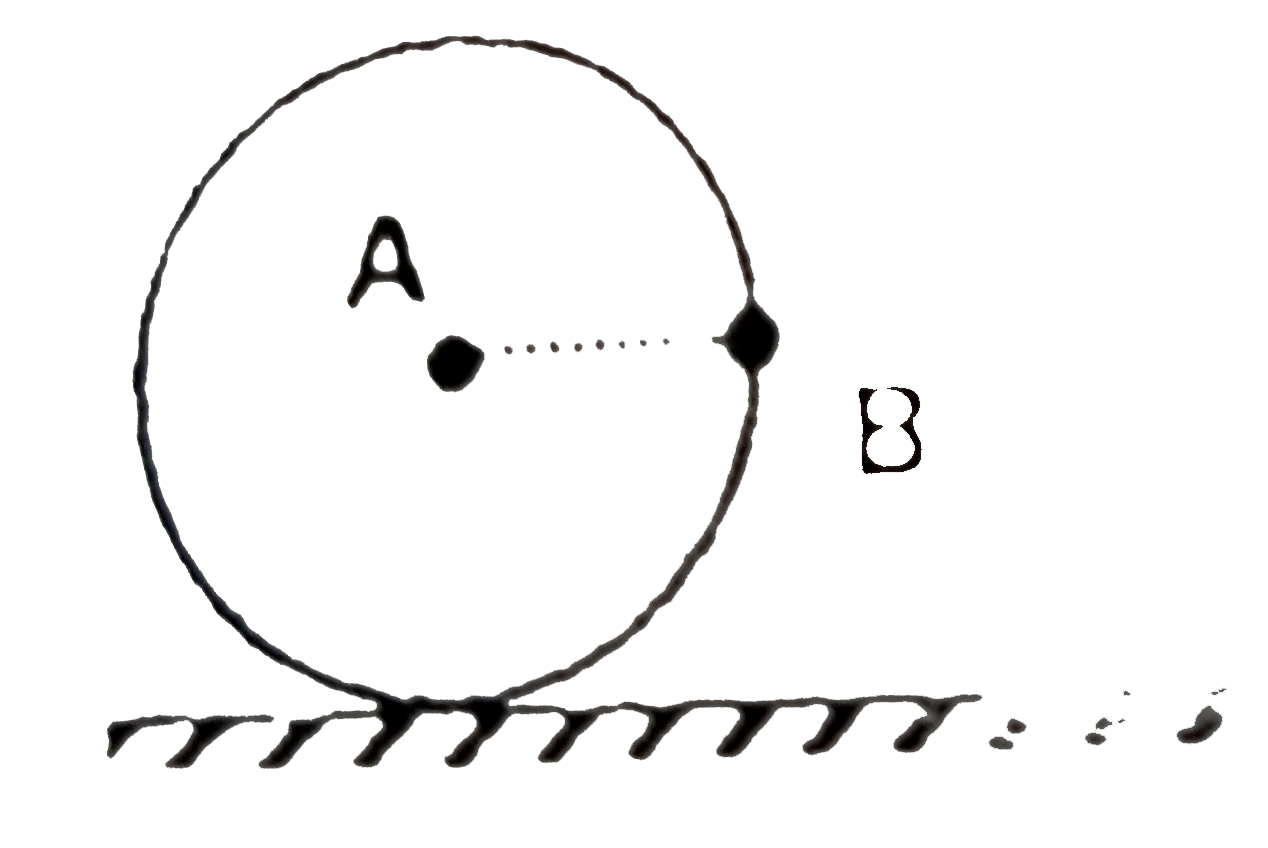
A particle of mass m is rigidly attached at A to a ring of mass 3m and radius r. The system is released from rest and rolls without sliding. The angular acceleration of ring just after release is

g4r
g6r
g8r
g2r
The correct Answer is:B
The distance of CM from the ring centre O. x=3m(0)+m(r)3m+m=r4
We can apply torque about point of contact as the ring is rolling, τp=Ipα
4mg(r4)=[(3mr2+mr2)+m(AP)2]α⇒mgr=[4mr2+m(√2r)2]α⇒mgr=6mr2α⇒g6r
Similar Questions
A small particle of mass m is attached at B to a hoop of mass m and radius r, whole system is placed on the rough horizontal ground. The system is released from rest when B is dierctly above A and rolls without slipping. Find the angular acceleration of the system at the instant when AB becomes horizontal as shown in the figure.
View SolutionA ring of mass m and radius R is placed on a rough inclined plane so that it rolls without slipping . Match the following table.



View Solution
Knowledge Check
A disc of mass m is connected with an ideal spring of stiffness k. If it is released from rest, it rolls without sliding on an inclination plane. The maximum elongation of the spring is:
 AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθk
AmgsinθkB2mgsinθ3kC3mgsinθkD2mgsinθkThe total energy of rolling ring of mass m and radius R is
A3/2mv2B1/2mv2Cmv2D5/2mv2A particle of mass m is released from rest and follows a particle as a function of time?
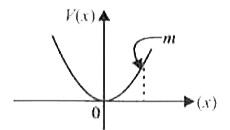 A
A B
B C
C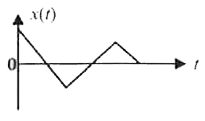 D
D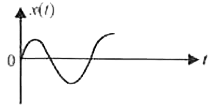
Two point masses of mass m and equal and opposite charge of magnitude q are attached on the corners of a non-conducting uniform rod of mass m and the system is released from rest in uniform electric field E as shown in figure from θ=53∘

(i) Find angular acceleration of the rod just after releasing
(ii) What will be angular velocity of the rod when it passes through stable equilibrium.
(iii) Find work required to rotate the system by 180∘.
View SolutionFigure-2.54 shows a block of mass m is placed on an inclined wedge of mass M If the system is released from rest find the acceleration of m and M.
View SolutionA small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):
View SolutionA small particle of mass m is fixed to the perimeter of a ring of same mass and radius r. The system comprising of particle and ring is placed on a horizontal plane. Friction is negligible on horizontal plane. Initially particle is at top most point, then the system is released from rest. Answer next two question when the particle is at the same height as the centre of ring aftr being released from top most point. Assume that the ring stays in vertical plane during its motion under consideration

Mark the CORRECT option(s):-
View SolutionA uniform disc of mass M and radius R is supported vertically by a pivot at its periphery as shown. A particle of mass M is fixed to the rim and raised to the highest point above the center. The system is released from rest and it can rotate about pivot freely. The angular speed of the system when the attached object is directly beneath the pivot, is
View Solution
