A ladder of length l and mass m is placed against a smooth vertical wall, but the ground is not smooth. Coefficient of friction between the ground and the ladder is μ. The angle θ at which the ladder will stay in equilibrium is
θ=tan−1(μ)
θ=tan−1(2μ)
θ=tan−1(μ2)
None of these
The correct Answer is:D
Rod is in equilibrium (but just about to slip)
⇒∑F=0⇒N1=mg and N2=μSN1⇒τabout any point=0
τabout bottom=mgl2cosθ−N2lsinθ=0
tanθ=mg2N2=mg2μ2mg⇒tanθ=12μS

Similar Questions
A uniform ladder of length 3.25 m and weight 250 N is placed against a smooth vertical wall with its lower end 1.25 m from the wall. If coefficient of friction between the ladder and the floor is 0.3, then, find the frictional force acting on the ladder at the point of contact between ladder and floor.
View SolutionA uniform ladder of length l rests against a smooth, vertical wall (figure). If the mass of the ladder is m and the the coefficient of static friction between the ladder and the ground is μs=0.375 and the minimum angle θmin at which the ladder does not slip.

A uniform ladder at rest, leading against a smooth wall. Th ground is rough.
View Solution
Knowledge Check
A ladder of length 5m is placed against a smooth wall as shown in figure. The coefficient or friction is μ between ladder and ground. What is the minimum value of μ , If the ladder is not to slip?
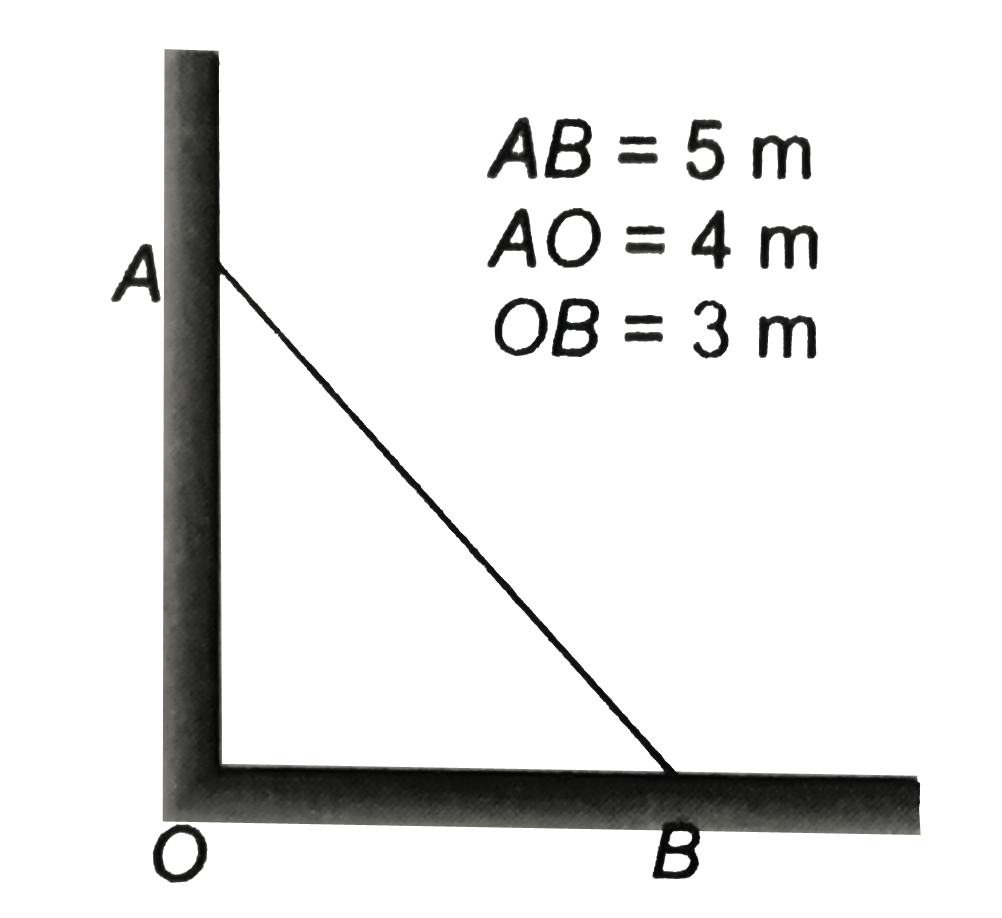 Aμ=12Bμ=14Cμ=38Dμ=58
Aμ=12Bμ=14Cμ=38Dμ=58A ladder of mass 10kg is held at reat against a smooth wall on a rough ground as shown in figure. The normal reaction between the wall and the ladder is
 A50NB50√3NC60√3ND100N
A50NB50√3NC60√3ND100NIf a ladder is not in balance against a smooth vertical wall, then it can be made in balance by :-
ADecreasing the length of ladderBIncreasing the length of ladderCIncreasing the angle of inclinationDDecreasing the angle of inclination
A ladder of mass M and length L stays at rest against a smooth wall. The coefficient of friction between the ground and the ladder is μ
(a) Let Fwall, W and Fg be the force applied by wall, weight of the ladder and force applied by ground on the ladder. Argue to show that the line of action of these three forces must intersect.
(b) Using the result obtained in (a) show that line of action of Fg makes an angle tan−1(2tanθ) with the horizontal ground where θ is the angle made by the ladder with the ground.
(c) Find the smallest angle that the ladder can make with the ground and not slip.
(d) You climb up the ladder, your presence makes the ladder more likely to slip. Where are you at A or B? C is the centre of mass of the ladder.
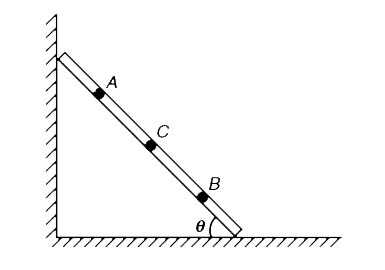
View SolutionA4m long ladder weighing 25kg rests with its upper and against a smooth wall and lower and on rought ground.What should be the minimum coefficient of friction between the ground and ladder for it to be inclined at 60∘ with the horizontal without slipping? (Takeg=10m/s2)
View SolutionA uniform ladder is placed against a wall, if the ground and wall are equally rough the coefficient of friction being tanθ limiting inclination of the ladder to the vertical is 2θ.
View SolutionA ladder wighing 300 N is placed against a smooth vertical wall having a coefficient of friction between it and the floor of 0.2. What is the maximum force of friction available at the point of contact between the ladder and the floor?
View SolutionA ladder, 10 metre long rests with one end against a smooth vertical wall and the other end on the ground which is rough, the coefficient of friction being 12. The foot of the ladder being 2 metre from the wall. A amn whose weight is 4 times that of the ladder can ascend before it be givens to slip is
View Solution