A slender rod of mass m and length L is pivoted about a horizontal axis through one end and released from rest at an angle of 30∘ above the horizontal. The force exerted by the pivot on the rod at the instant when the rod passes through a horizontal position is

√10gmg along horizontal
mg along vertical
√104mg along a line making an angle of tan−1(13) with the horizontal.
√104=mg along a line making an angle of tan−1(3) with the horizontal.
The correct Answer is:C
The angular velocity of the rod about pivot when it passes through horizontal position is given by
mg×L2sin30∘=mL23×ω22,ω=√3g2L

Radial accleration of the cenre of mass (as centre of mass is moving in a circle of radius L/2) is given by ar=ω2L2=3g4
Torque about pivot, in horizontal position, is,
τ=mgL2=Iα,α=mgL/2mL2/3=3g2L
Tangential acceleration of the centre of mass, at=L2α3g4

mg−N1=mat⇒N1=mg−3mg4=mg4
N2=mar=3mg4 ∴N=√N21+N22=√104=mg
Angle with horizontal is tan−1(N1N2)=√104mg
Angle with horizontal is tan−1(N1N2)=tan−1(13)
Similar Questions
A rod of length l is pivoted about a horizontal , frictionless pin through one end. The rod is released from ret in a vertical position. Find the velocity of the CM of the rod when the rod is inclined at an angle θ from the vertical.

View SolutionA uniform rod AB of mass 3m and length 4l, which is free to turn in a vartical plane about a smooth horizontal axis through A, is released from rest when horizontal When the rod first impulse exerted by the peg on the rod it.
(a). The rod is brought to rest by the peg.
(b). The rod rebounds and next comes to instantaneous rest inclined to the downward vertical at an angle π3 radian.
View Solution
Knowledge Check
A uniform disc of mass M and radius R is pivoted about a horizontal axis passing through its edge. It is released from rest with its centre of mass at the same height as the pivot.
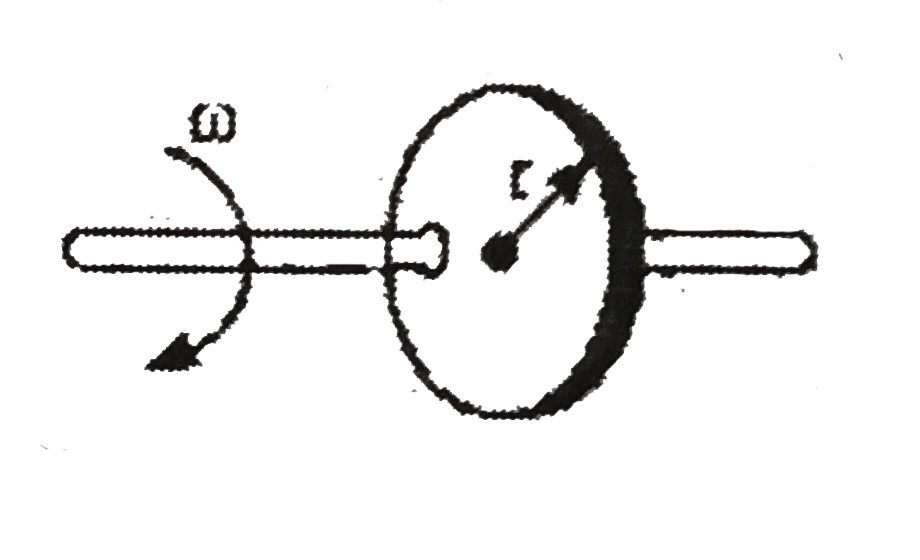 AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zero
AThe angular velocity of disc when its centre of mass is directly below the pivot is √4g3rBThe force exerted by the pivot at this instant is 73mgCAngular momentum of disc is conservedDAngular acceleration of disc at the given instant is zeroA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
 Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14
Amg4B3mg2cosθCmg4√9cos2θ+14Dmg2√9cos2θ+14A slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
AJBJ2CJ3DInformation is insufficient
A uniform slender bar B of mass m and length L supported by a firctionless m and length L supported by a firctionless pivot at A is released from rest at its vertical position as shown the figure. Calculate the reaction at pivot when the bar just acquires the horizontal position shown dotted.

View SolutionA uniform slender rod of mass M and length L is pivoted at its end. The rod is released from its nearly vertical position. What is the reaction at the pivot when the rod reaches the horizontal position? If the support is withdrawn at this instant, describe the subsequent motion of the rod.
View SolutionA rod AB of mass m and length L is rotating in horizontal plane about one of its ends which is pivoted. The constant angular speed with which the rod is rotating is ω. The force applied on the rod by the pivot is
View SolutionOne end of a straight uniform 1m long bars pivoted on horizontal table. It is released from rest when it makes an angle 30∘ from the horizontal (see figure ) . Velocity of end point of the rod when it hits the table is given as √nms−1,where n is an integer.The value of n is _______________

View SolutionA rod of length 50cm is pivoted at one end. It is raised such that if makes an angle of 30∘ from the horizontal as shown and released from rest. Its angular speed when it passes through the horizontal (in rads−1) will be (g=10ms−2)

View Solution