When two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
In series ,i=2E2+R⇒J1=i2r=(2E2+R)2. R in parallel i=E0.5+R⇒J2=i2R=(E0.5+R)2.R
J1J2=2.25=5(0.5+R)2(2+R)2or1.5=2(0.5+R)(2+R) On solving we get R=4Ω
Similar Questions
When two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance in 1 second?
View Solution
Knowledge Check
Two identical batteries, each of EMF 2V and internal resistance r=1Ω are connected as shown. the maximum power that can be developed across R using these batteries is :
 A3.2WB8.2WC2WD4W
A3.2WB8.2WC2WD4WTwo identical batteries, each of emf 2V and internal resistance r=1Ω are connected as shown. The maximum power that can be developed across R using these batteries is
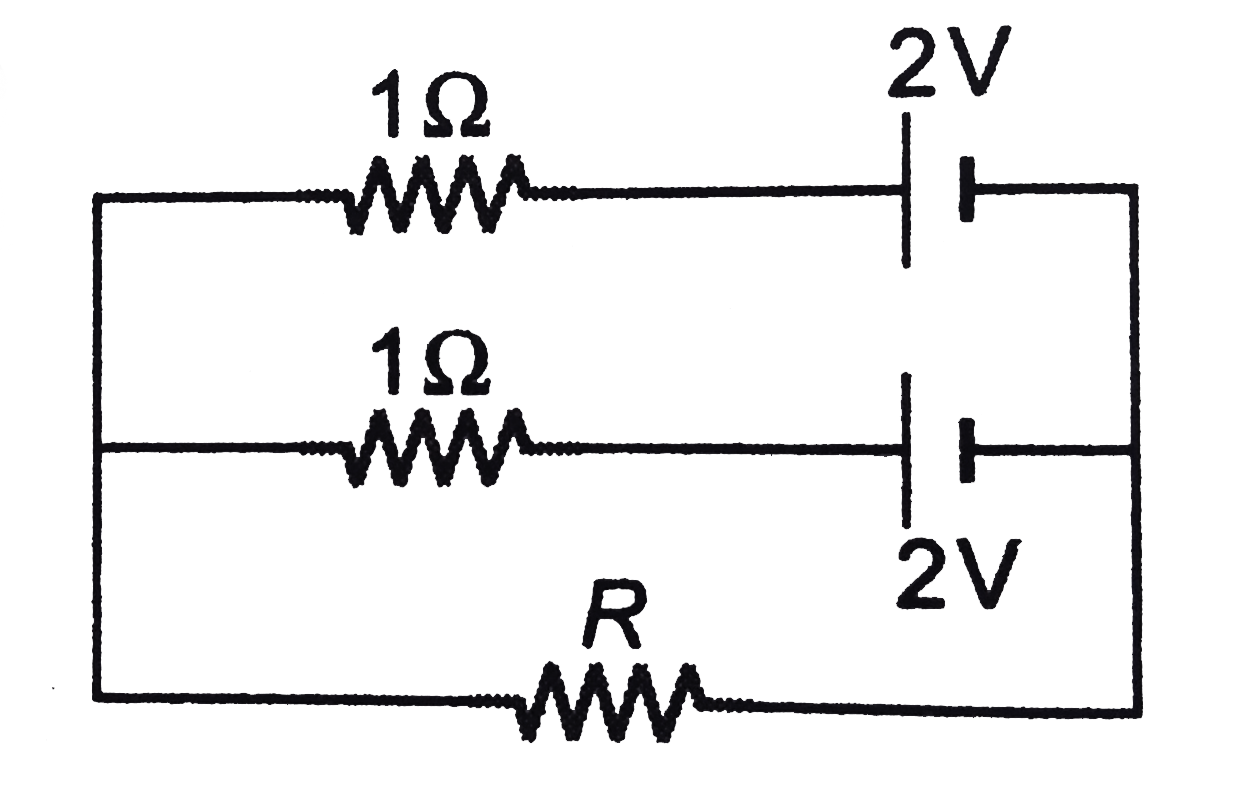 A3.2WB8.2WC2WD4W
A3.2WB8.2WC2WD4Wn identical calls, each of internal resistance (r) are first connected in parallel and then connected in series across a resistance (R). If the current through R is the same in both cases, then
AR=r2Br=R2CR=rDr=0
A galvanometer, together with an unknown resistance in series, is connected across two identical batteries of each 1.5V. When the batteries are connected in series,the galvanometer records a current of 1A, and when the batteries are connected in parallel, the current is 0.6A. In this case, the internal resistance of the battery is 1/'∗'Ω.
What is the value of '**'?
View SolutionFive identical cells each of internal resistance 1Ω and emf 5V are connected in series and in parallel with an external resistance 'R' . For what value of 'R', current in series and parallel combination will remain the same ?
View SolutionThree batteries having emfs and internal resistances as shown in figure are connected across a resistor of 2Ω. The reading of ammeter is
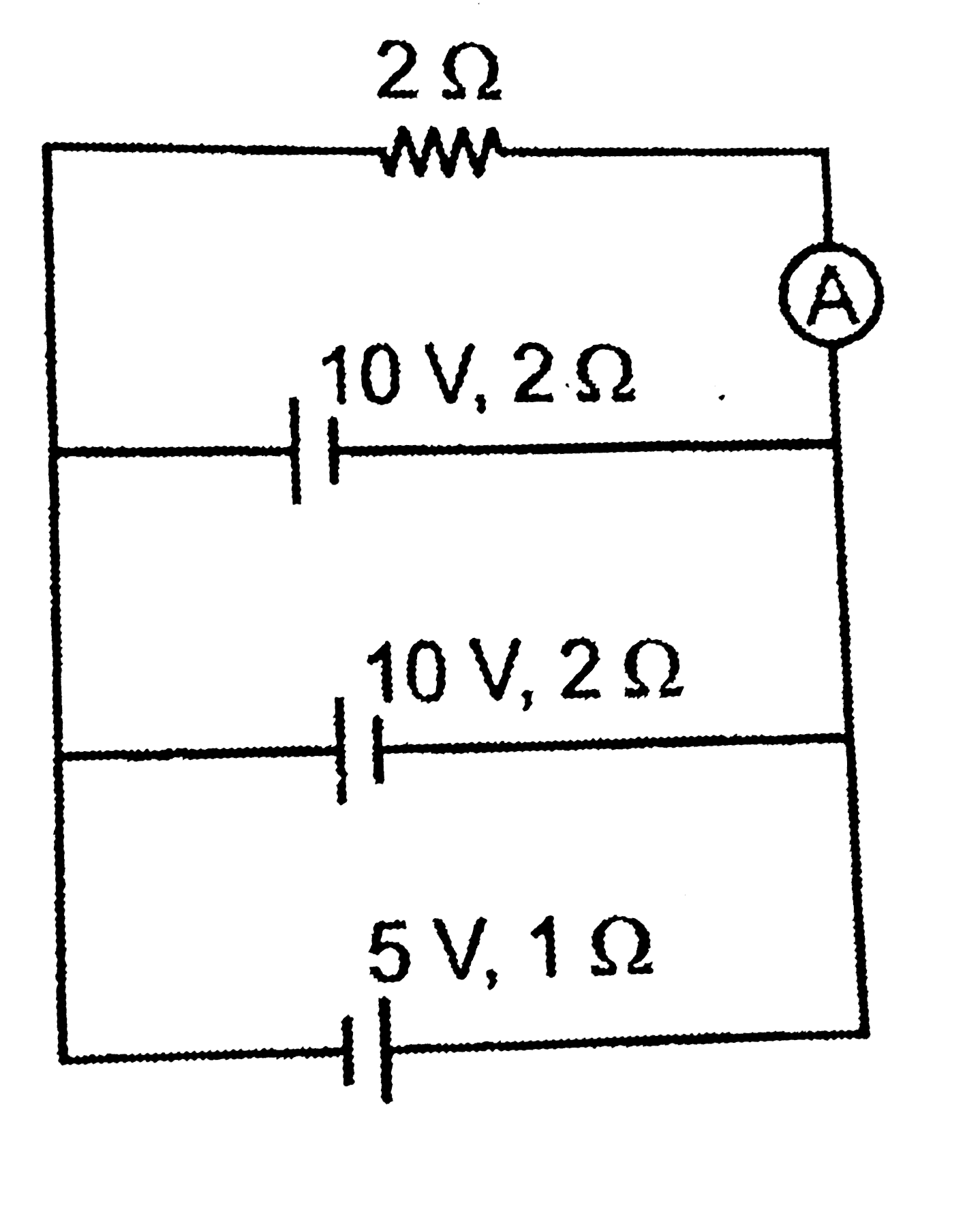
View SolutionTwo cells , each of emfE and internal resistance r, are connected in parallel across a resistor R. The power delivered to the resistor is maximum if R is equal to
View SolutionTwo coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
View Solution
