Two coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
500 J, 500 J
320 J, 640 J
320 J, 320 J
None of these
The correct Answer is:B
Total resistance of the circuit, R=3Ω+6Ω=9Ω
Current in the circuit, I=VR=12V9Ω=(4/3)A
Since the resistances are in series, same current flows in each resistance.
Electric energy consumed by R1(=3Ω) in 1 minute, i.e.,
W1=I2R1t=(4/3A)2(3Ω)(60s)=320J (1min=60s)
Electric energy consumed by in R2(=6Ω)=(4/3A)2(6Ω)(60s)=640J.
Topper's Solved these Questions
Similar Questions
Two resistances of values 150±2Ω and 250±5Ω are connected in series. Find their equivalent resistance.
View Solution(a) A cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance 100Ω. When a voltmeter is connected across the 100Ω resistance the ammeter reading is 0.04A. Find the voltage read by the voltmeter and its resistance. Had the voltmeter been an ideal one, what would have its reading ?
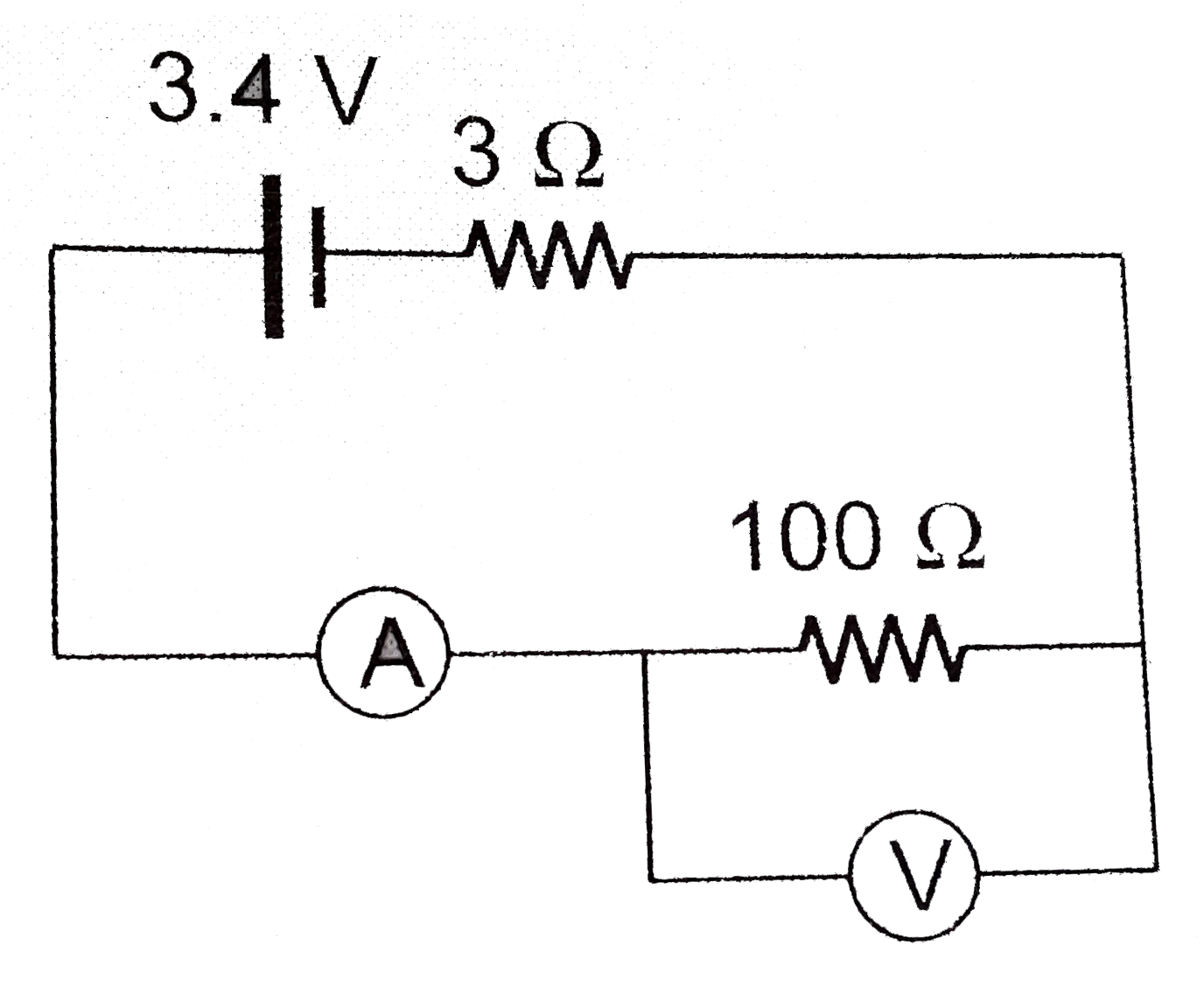
(b) Two resistances of 100Ω and 200Ω are connected in series with battery of emf 4V and negligible internal resistance. A voltmeter of resistance 200Ω is used to measure voltemeter of resistances separately. Calculate the voltmeter indicated.
( c) In the circuit shown, a voltmeter reads 30V when it is connected across the 400Ω resistance. Calculate what the same voltmeter will read when it is connected across the 300Ω resistance ?
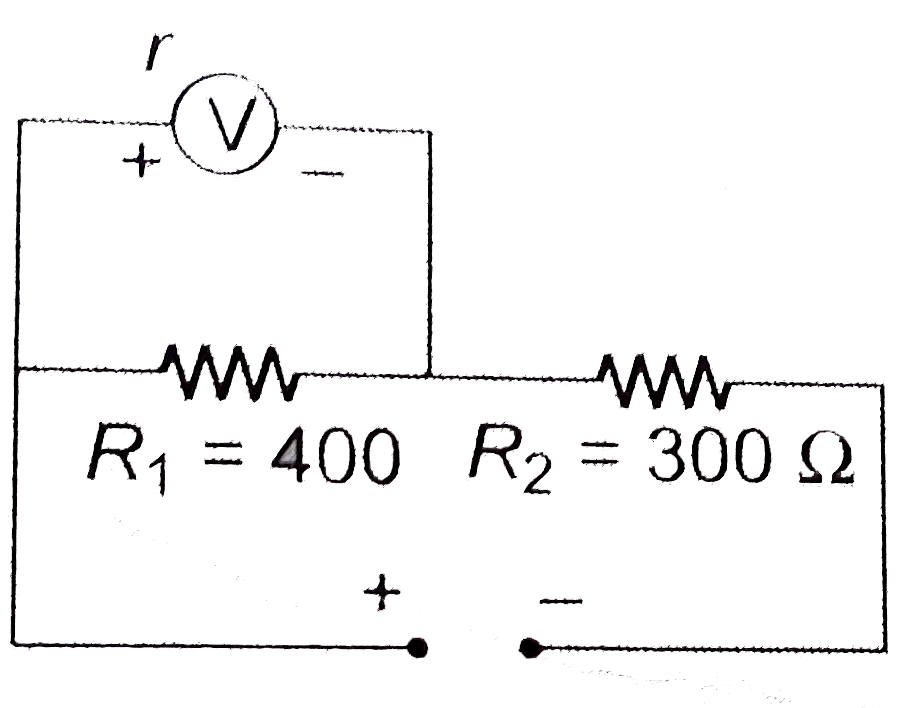
(d) An ammeter and a voltmeter are connected in series to a battery of emf E=6.0V. When a certain resistance is connected in parallel with the voltmeter. the reading of the ammeter is doubled. while voltmeter reading is reduced to half. Find the voltmeter reading after the connection of the resistance.
View Solution
Knowledge Check
two heading coils of resistances 10Ωand20Ω are connected in parallel and connected to a battery of emf 12 V and internal resistance 1Ω Thele power consumed by the n are in the ratio
A1:4B1:3C2:1D4:1Two heating coils of resistance 10Ωand20Ω are connected in parallel and connected to a battery of emf 12V and internal resistance 1Ω. The power consumed by them is in the ratio
A1:4B1:3C2:1D4:1Two resistors of 6Ω and 9Ω are connected in series to a 120 V source. The power consumed by the 6Ω resistor is
A384 WB576 WC1500 WD1800 W
Six identical resistance of resistance 20Ω each are connected in the form of a hexagon across a battery of 3 V. Find the current through the battery when the battery is connected (i) between any two adjacent vertices. (ii) across any two opposite vertices.
View SolutionTwo resistances R1=100±3ΩandR2=200±4Ω are connected in series . Find the equivalent resistance of the series combination.
View SolutionA bulb used in a car is rated 12 V, 48 W. Find the energy consumed in one minute when the bulb is connected to a 6 -V battery.
View SolutionTwo resistors of resistances R1=(300±3)Ω and R2=(500±4)Ω are connected in series. The equivalent resistance of the series combination is
View SolutionTwo resistors of 500Ω and 300Ω are connected in series with a battery of emf 20V.A voltmeter of resistance 500Ω is used to measure the p.d across the 500Ω resistor. The error in the measurement is.
View Solution

