Six identical resistance of resistance 20Ω each are connected in the form of a hexagon across a battery of 3 V. Find the current through the battery when the battery is connected (i) between any two adjacent vertices. (ii) across any two opposite vertices.
To solve the problem, we will break it down into two parts as specified in the question.
Part (i): Battery connected between any two adjacent vertices
1. Identify the Configuration:
- We have six resistors (each of 20 Ω) arranged in a hexagon. When the battery is connected between two adjacent vertices, we can visualize the circuit.
2. Label the Resistors:
- Let's label the resistors as R1, R2, R3, R4, R5, and R6, each having a resistance of 20 Ω.
3. Determine the Equivalent Resistance:
- The two resistors (R1 and R2) directly connected to the battery are in series. The remaining resistors (R3, R4, R5, R6) form a parallel connection.
- The total resistance in series (R1 + R2) = 20 Ω + 20 Ω = 40 Ω.
- The remaining four resistors (R3, R4, R5, R6) can be simplified as follows:
- R3 and R4 are in series, and R5 and R6 are in series. Thus, R3 + R4 = 20 Ω + 20 Ω = 40 Ω and R5 + R6 = 20 Ω + 20 Ω = 40 Ω.
- Now, R3 + R4 (40 Ω) is in parallel with R5 + R6 (40 Ω).
- The equivalent resistance of two resistors in parallel is given by:
Req=R1⋅R2R1+R2=40⋅4040+40=160080=20Ω
4. Total Equivalent Resistance:
- The total equivalent resistance in the circuit is:
Rtotal=Rseries+Rparallel=40Ω+20Ω=60Ω
5. Calculate the Current:
- Using Ohm's Law (V = IR), we can find the current (I) through the battery:
I=VRtotal=3V60Ω=0.05A
Part (ii): Battery connected across any two opposite vertices
1. Identify the Configuration:
- When the battery is connected across two opposite vertices, we can visualize the circuit again.
2. Determine the Equivalent Resistance:
- In this case, the resistors can be grouped into two sets of three resistors in series:
- The top three resistors (R1, R2, R3) and the bottom three resistors (R4, R5, R6) are in series.
- The total resistance for each set is:
Rtop=R1+R2+R3=20Ω+20Ω+20Ω=60Ω
Rbottom=R4+R5+R6=20Ω+20Ω+20Ω=60Ω
- Now, these two sets of resistors are in parallel:
Req=Rtop⋅RbottomRtop+Rbottom=60⋅6060+60=3600120=30Ω
3. Calculate the Current:
- Again, using Ohm's Law:
I=VReq=3V30Ω=0.1A
Final Answers:
- (i) The current through the battery when connected between any two adjacent vertices is 0.05 A.
- (ii) The current through the battery when connected across any two opposite vertices is 0.1 A.
- We have six resistors (each of 20 Ω) arranged in a hexagon. When the battery is connected between two adjacent vertices, we can visualize the circuit.
- Let's label the resistors as R1, R2, R3, R4, R5, and R6, each having a resistance of 20 Ω.
- The two resistors (R1 and R2) directly connected to the battery are in series. The remaining resistors (R3, R4, R5, R6) form a parallel connection.
- The total resistance in series (R1 + R2) = 20 Ω + 20 Ω = 40 Ω.
- The remaining four resistors (R3, R4, R5, R6) can be simplified as follows:
- R3 and R4 are in series, and R5 and R6 are in series. Thus, R3 + R4 = 20 Ω + 20 Ω = 40 Ω and R5 + R6 = 20 Ω + 20 Ω = 40 Ω.
- Now, R3 + R4 (40 Ω) is in parallel with R5 + R6 (40 Ω).
- The equivalent resistance of two resistors in parallel is given by:
Req=R1⋅R2R1+R2=40⋅4040+40=160080=20Ω
- The total equivalent resistance in the circuit is:
Rtotal=Rseries+Rparallel=40Ω+20Ω=60Ω
- Using Ohm's Law (V = IR), we can find the current (I) through the battery:
I=VRtotal=3V60Ω=0.05A
- When the battery is connected across two opposite vertices, we can visualize the circuit again.
- In this case, the resistors can be grouped into two sets of three resistors in series:
- The top three resistors (R1, R2, R3) and the bottom three resistors (R4, R5, R6) are in series.
- The total resistance for each set is:
Rtop=R1+R2+R3=20Ω+20Ω+20Ω=60Ω
Rbottom=R4+R5+R6=20Ω+20Ω+20Ω=60Ω
- Now, these two sets of resistors are in parallel:
Req=Rtop⋅RbottomRtop+Rbottom=60⋅6060+60=3600120=30Ω
- Again, using Ohm's Law:
I=VReq=3V30Ω=0.1A
- (i) The current through the battery when connected between any two adjacent vertices is 0.05 A.
- (ii) The current through the battery when connected across any two opposite vertices is 0.1 A.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - CONCEPTUAL QUESTIONS
35 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - TOUGH AND TRICKY PROBLEMS
23 Videos
- CURRENT ELECTRICITYBOOK - MODERN PUBLICATIONCHAPTER - CURRENT ELECTRICITYEXERCISE - Chapter Practice Test
15 Videos
- ATOMS BOOK - MODERN PUBLICATIONCHAPTER - ATOMS EXERCISE - Chapter Practice Test
16 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - MODERN PUBLICATIONCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - CHAPTER PRACTICE TEST
15 Videos
Similar Questions
Six 18.0Ω resistors are connected in parallel across a 12.0V ideal battery. What is the current through the battery?
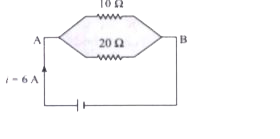
View SolutionTwo resistors of resistance 10Ω and 20Ω are connected in parallel. A battery supplies 6 A of current to the combination. Calculate the current in each resistor.
View Solution
Knowledge Check
Two coils of resistances 3Ωand6Ω are connected in series across a battery of emf12V. Find the electrical energy consumed in 1 minute in each resistance when these are connected in series.
A500 J, 500 JB320 J, 640 JC320 J, 320 JDNone of theseA series combination of two resistors 1Ω each is connected to a 12 V battery of internal resistance 0.4Ω. The current flowing through it will be
A3.5AB5AC6AD10AWhen a resistance of 2 ohm is placed across a battery the current is 1 A and when the resistance across the terminals is 17 ohm, the current is 0.25A. The emf of the battery is
A4.5 VB5VC3VD6V
Two resistors 4Ωand6Ω connected in parallel. The combination is connected across a 6V battery of negligible resistance. Calculate
(a) the current through the battery
(b) current through each resistor.
View SolutionWhen two identical batteries of internal resistance 1Ω each are connected in series across a resistor R, the rate of heat produced in R is J1. When the same batteries are connected in parallel across R, the rate is J_2 = 2.25 J_2thenthevalueofR∈Omega is
View SolutionA wire of resistance 4Ω is connected to a battery having an internal resistance of 1Ω For a current of 6 A to flow through the circuit what should be the emf of the battery ?
View SolutionTwo equal resistances are connected in seires across a battery and consume a power P If these are connected in parallel, then power consumed will be
View SolutionTwo identical batteries, each of EMF 2V and internal resistance r=1Ω are connected as shown. the maximum power that can be developed across R using these batteries is :

View Solution
