A recantangular frame is to be suspended symmetrically by two strings of equal length on two supports (figure).It can be done in one of the following three ways:

A

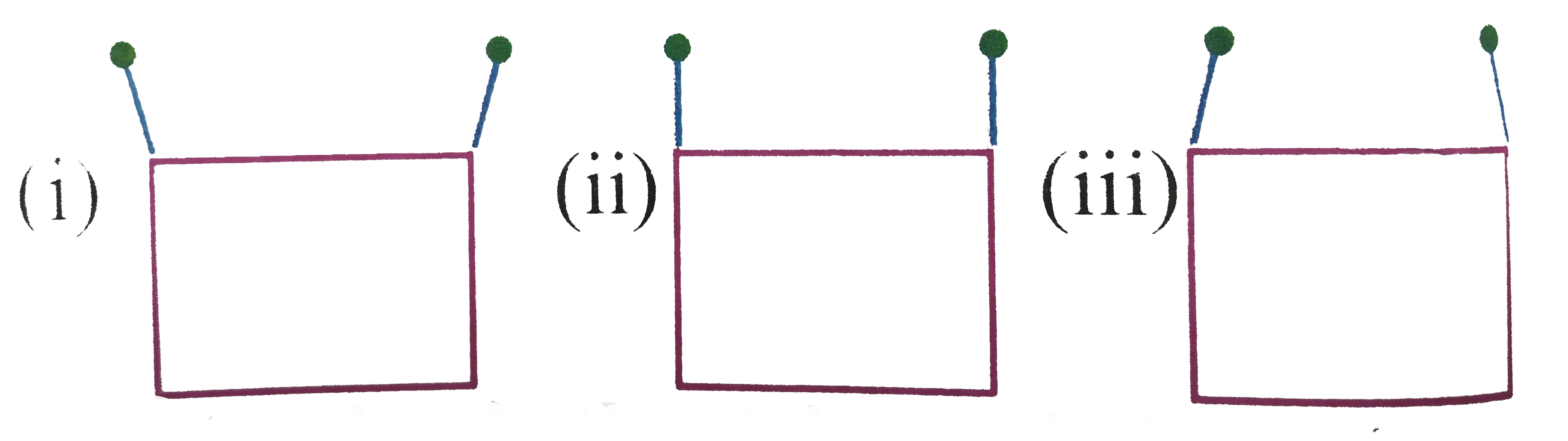
the same in all cases

B

least in (a)

C

least in (b)

D

least in (c )

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Consider the FBD diagram of the rectangular frame

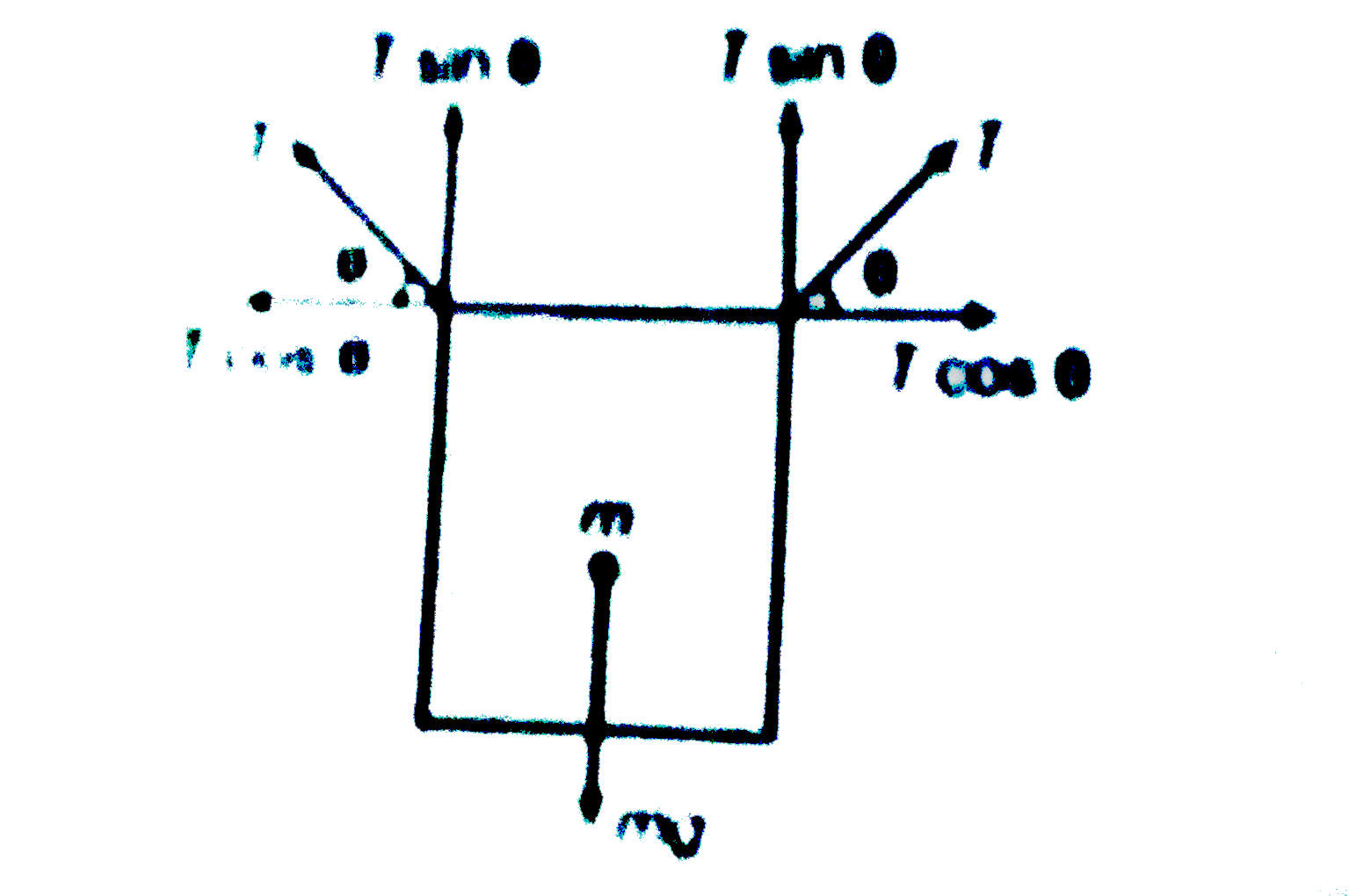
Balancing vertical forces $2 T \sin θ - m g = 0 [T is tension in the string]$
$\Rightarrow 2 T \sin θ = m g .....(i)$
Total horizontal force = $T \cos θ - T \cos θ = 0$
Now from Eq. (i), $T = \frac{m g}{2 \sin θ}$
As mg is constant
$\Rightarrow T \propto \frac{1}{\sin θ} \Rightarrow T_{max} = \frac{m g}{2 {\sin θ}_{min}}$
${\sin θ}_{min} = 0 \Rightarrow θ_{min} = 0$
No option matches with $θ = 0^{\circ}$
$T_{min} = \frac{m g}{2 {\sin θ}_{max}} (Since, {\sin θ}_{max} = 1)$
${\sin θ}_{max} = 1 \Rightarrow θ = 90^{\circ}$
Matches with option (b)
Hence, tension is least for the case (b).
Note We should be careful when measuring the angle, it must be in the direction as given in the diagram.

|

Updated on:21/07/2023

Class 11 PHYSICS PROPERTIES OF SOLIDS AND FLUIDS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One

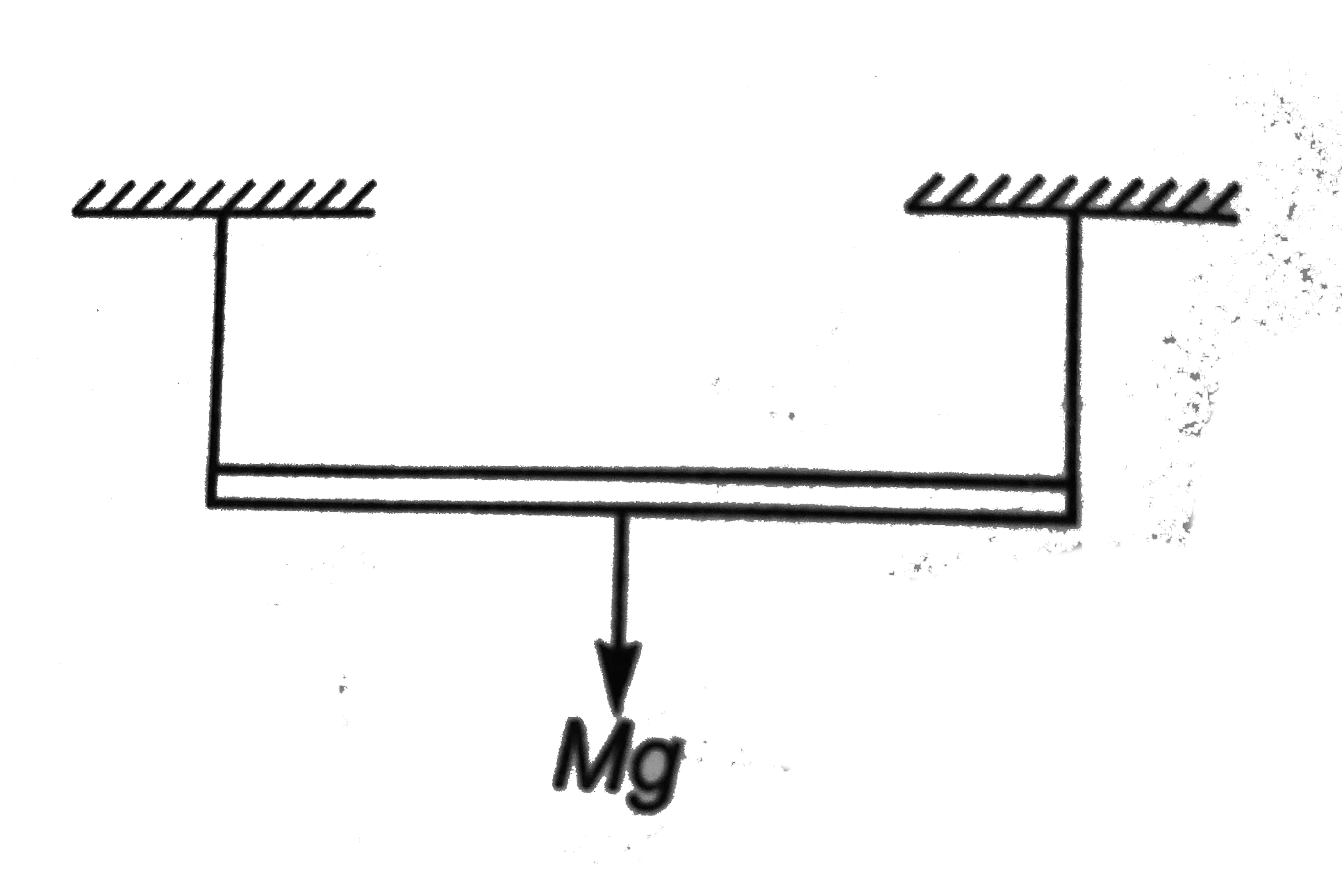
A rod is supported horizontally by means of two strings of equal length as shown in figure. If one of the string is cut. Then tension in other string at the same instant will.
Aremains unaffected
Bincrease
Cdecrease
Dbecome equal to weight of the rod.
Question 2 - Select One
A uniform rod of length 3L and mass m is suspended from a horizontal roof by two strings of length L and 2L as shown. Then the tension in the left string of length L is :

Amg
B $\frac{m g}{4}$
C $\frac{m g}{2}$
D $\frac{m g}{3}$
Question 3 - Select One
Two spherical objects each of radii R and masses m1 and m2 are suspended using two strings of equal length L as shown in the figure $(R < < L)$ . The angle, $θ$ which mass $m_{2}$ makes with the vertical is approximately -

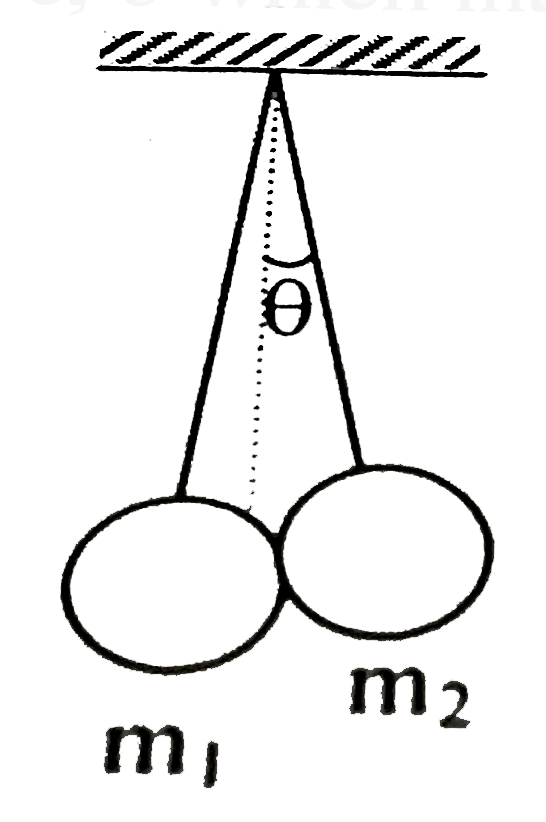A $\frac{m_{1} R}{(m_{1} + m_{2}) L}$
B $\frac{2 m_{1} R}{(m_{1} + m_{2}) L}$
C $\frac{2 m_{2} R}{(m_{1} + m_{2}) L}$
D $\frac{m_{2} R}{(m_{1} + m_{2}) L}$

NCERT EXEMPLAR-MECHANICAL PROPERTIES OF SOLIDS-LONG SHORT ANSWER TYPE QUESTION

Home
Ask Doubt
Profile