A parallel plate capacitor is of area 6 cm2 and a separation 3 mm. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constant K1=10, K2=12andK3=14. The dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be :
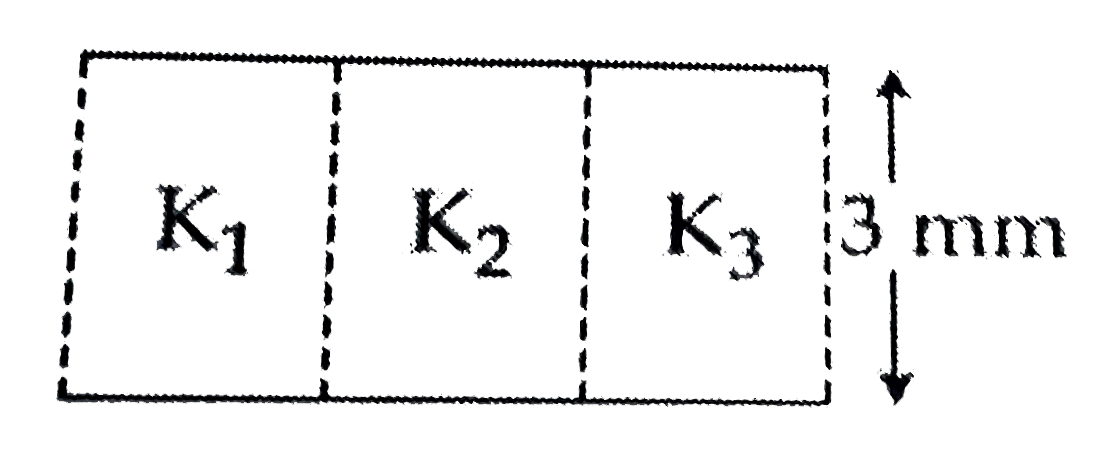
14
36
12
4
The correct Answer is:C
C=10×A3ε0d+12×A3ε0d+14×A3ε0d=36×A3ε0d=12Aε0d.
Similar Questions
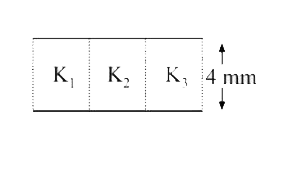
A parallel plate capacitor is of area 6cm2 and a separation 4 mm. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constants K1=7,K2=15 and K3=5 . The equivalent dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be______.
View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constant K1,K2 and K3 as shown in fig. If a single dielectric material is to be used to have the same effective capacitance as the above combination then its dielectric constant K is given by :
View Solution
Knowledge Check
A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1,k2 and k3 as shown. If a single dielectric naterial is to be used have the same capacitance C in this capacitor, then its dielectric constant k is given by
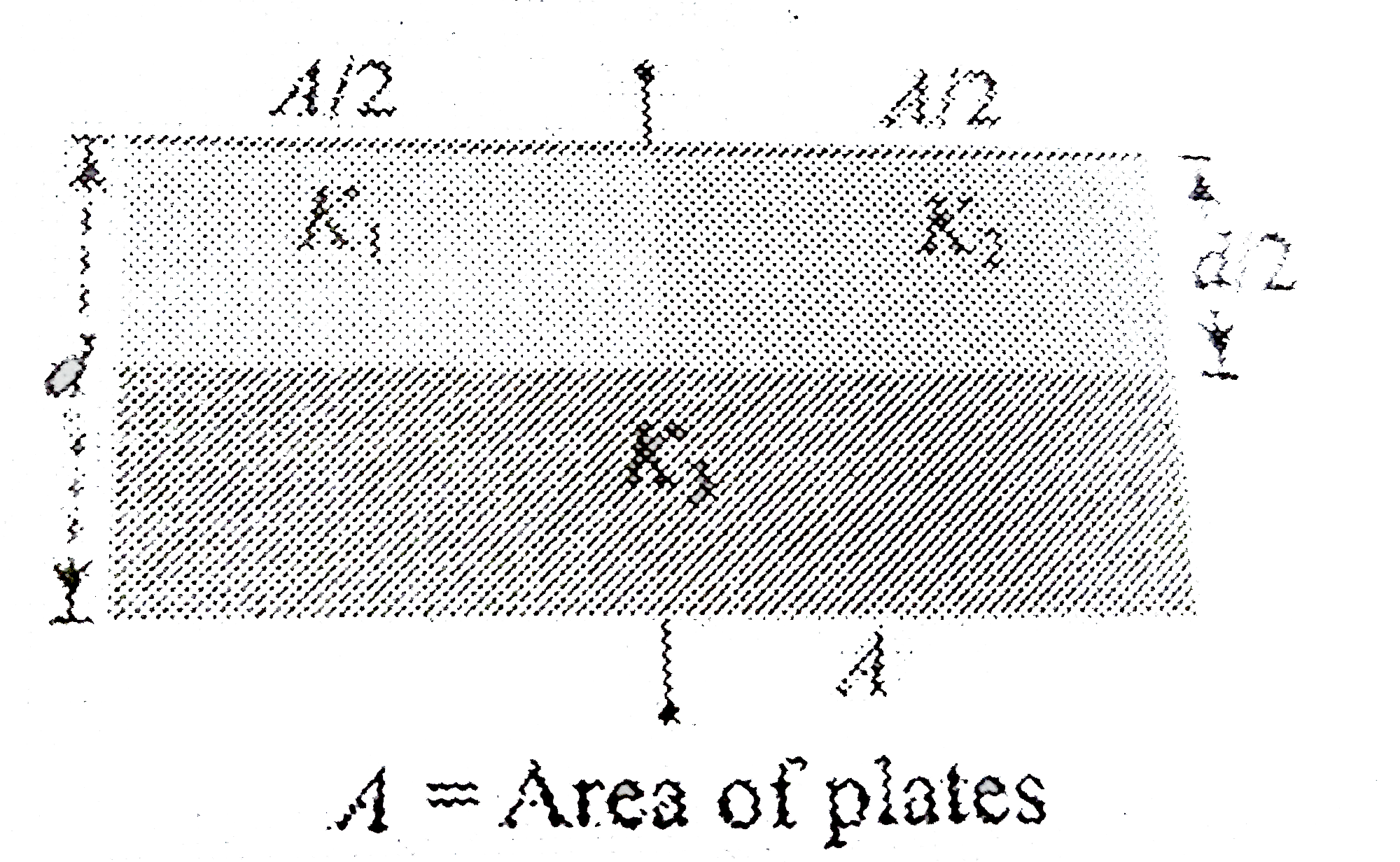 A1k=1k2+1k2+12k3B1k=1k2+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1+k2+2k3
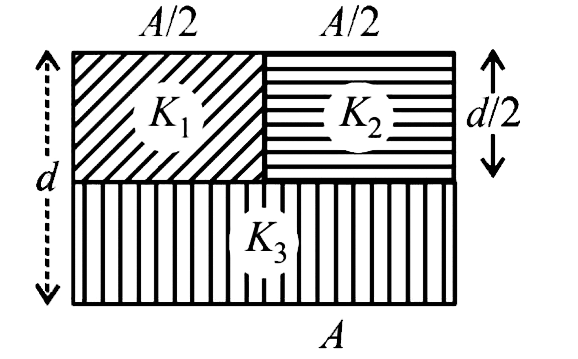
A1k=1k2+1k2+12k3B1k=1k2+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1+k2+2k3A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
 A(a) 1K=1K1+1K2+12K3B(b) 1K=1K1+K2+12K3C(c) K=K1K2K1+K2+2K3D(d) K=K1+K2+2K3
A(a) 1K=1K1+1K2+12K3B(b) 1K=1K1+K2+12K3C(c) K=K1K2K1+K2+2K3D(d) K=K1+K2+2K3A parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by
 AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
In the figure a capacitor is filled with dielectrics K1,K2 and K3. The resultant capacitance is
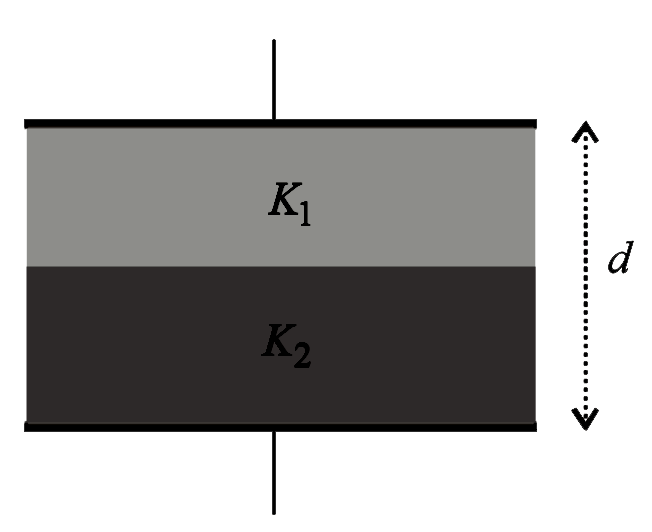
View SolutionThe space between parallel plate capacitors is filled with four dielectrics of equal dimensions but of dielectric constants K1,K2,K3andK4 respectively. If K is the dielectric constant of a single dielectric that must be filled between capacitor plates to have the same capacitance between A and B. Then we must have

View SolutionA parallel plate capacitor has plate area A and plate separation d. The space between the plates is filled up to a thickness x<d with a dielectric constant K. Calculate the capacitance of the system.

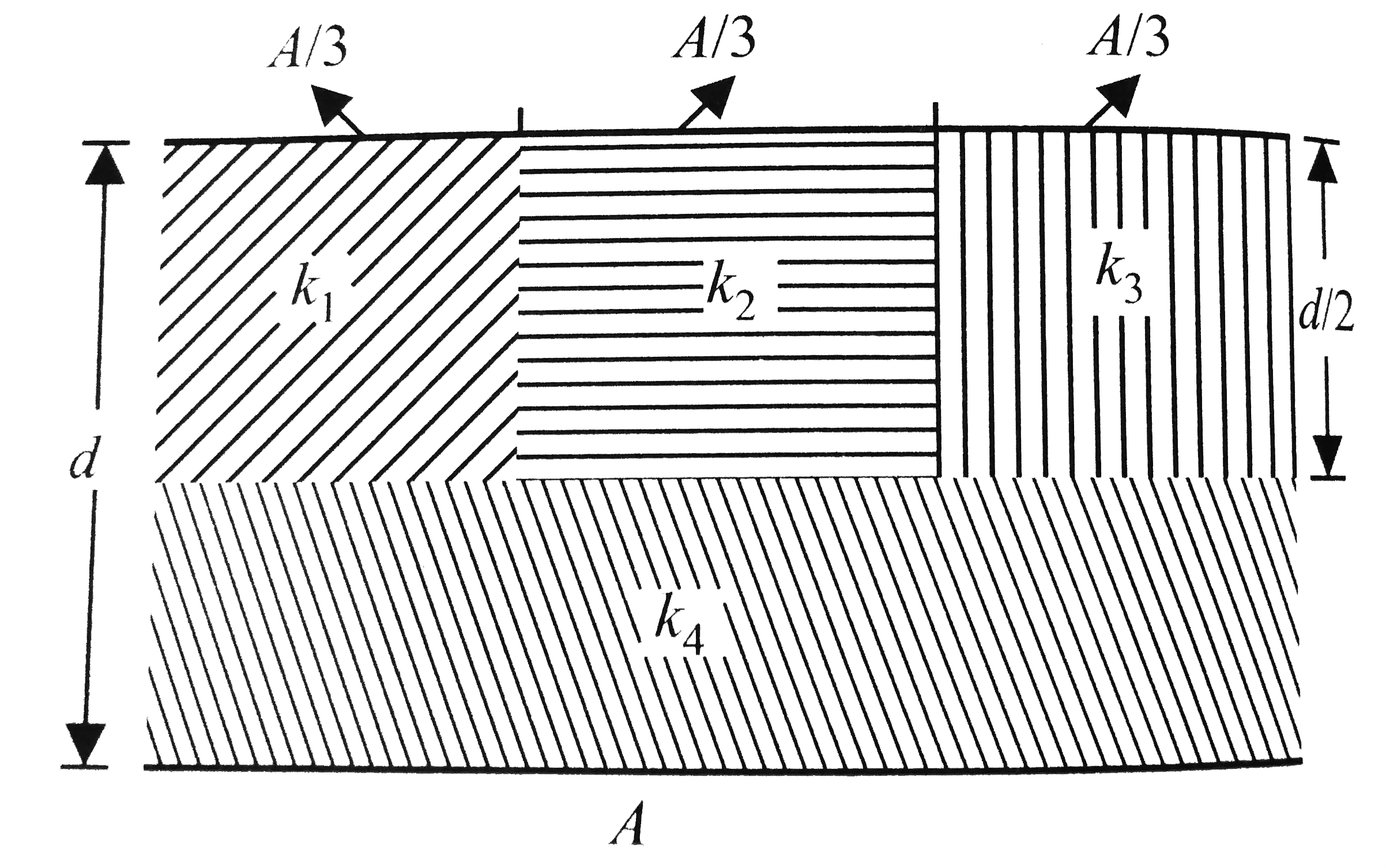
View SolutionA parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
View SolutionA parallel plate capacitor of plate area A and separation d is filled with two materials each of thickness d2 and dielectric constants ∈1 and ∈2 respectively. The equivalent capacitance will be

View Solution
