A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constant K1,K2 and K3 as shown in fig. If a single dielectric material is to be used to have the same effective capacitance as the above combination then its dielectric constant K is given by :
Let C=∈0Ad,C1=K1=∈A2d2=K1C
C2=K2∈0A2d2=K2C,
C3=K3∈0A2d2,=K3C,C3,=K3∈0A2d2,=K3C

The equivalent circuit as shown

Ceff=C1C3C1+C3+C2C3C2+C3
=(K1εA/2d/2)(K3εA/2d/2)(K1εA/2d/2+K3εA/2d/2)+(K2εA/2d/2)(K2εA/2d/2)(K2εA/2d/2+K2εA/2d/2)
Ceff=(K1K3K1+K3+K2K3K2+K3)C
Keff=(K1K3K1+K3+K2K3K2+K3).
Topper's Solved these Questions
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:C.U.Q
Explore 54 Videos
- CAPACITANCEBook:NARAYNAChapter:CAPACITANCEExercise:Assertion & Reasoning
Explore 16 Videos
- ATOMS Book:NARAYNAChapter:ATOMS Exercise:EXERCISE -4
Explore 47 Videos
- COMMUNICATION SYSTEMBook:NARAYNAChapter:COMMUNICATION SYSTEMExercise:Level-II(H.W)
Explore 25 Videos
Similar Questions
A parallel plate capacitor is of area 6 cm2 and a separation 3 mm. The gap is filled with three dielectric materials of equal thickness (see figure) with dielectric constant K1=10, K2=12andK3=14. The dielectric constant of a material which when fully inserted in above capacitor, gives same capacitance would be :
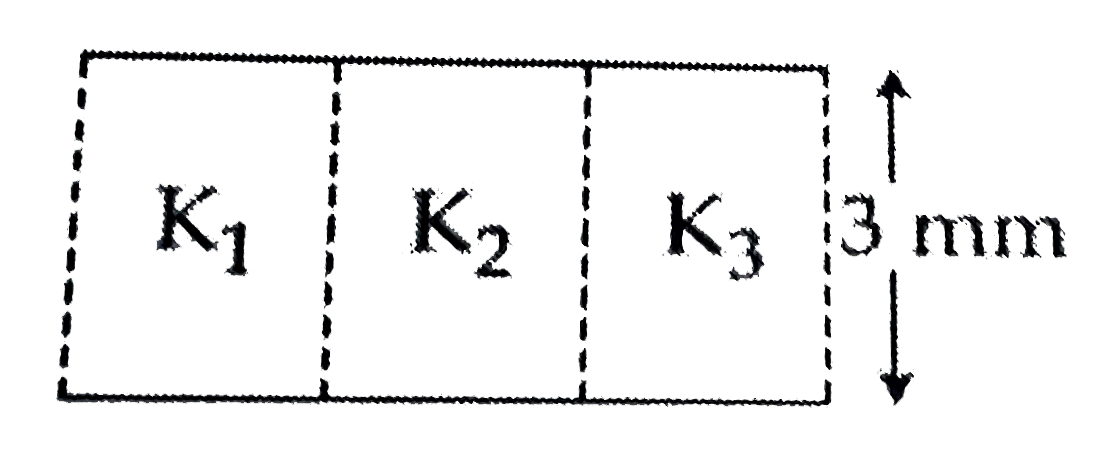
View SolutionAn air capacitor of capacitance C plate area A and plate separation d has been filled with three dielectrics of constant k1=3,k2=6 and k3=4 as shown in figure . What is the new capacitance ?

View Solution
Knowledge Check
A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1k2andk3 as shown in the following figure. If a single dielectric material is to be used to have the same capacitance C in this capacitor then its dielectric constant k is given by
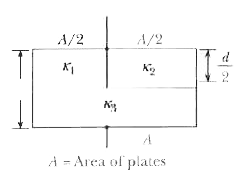 A1k=1k1+1k2+12k3B1k=1k1+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1k3k1+k3+k2k3k2+k1
A1k=1k1+1k2+12k3B1k=1k1+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1k3k1+k3+k2k3k2+k1A parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1,k2 and k3 as shown. If a single dielectric naterial is to be used have the same capacitance C in this capacitor, then its dielectric constant k is given by
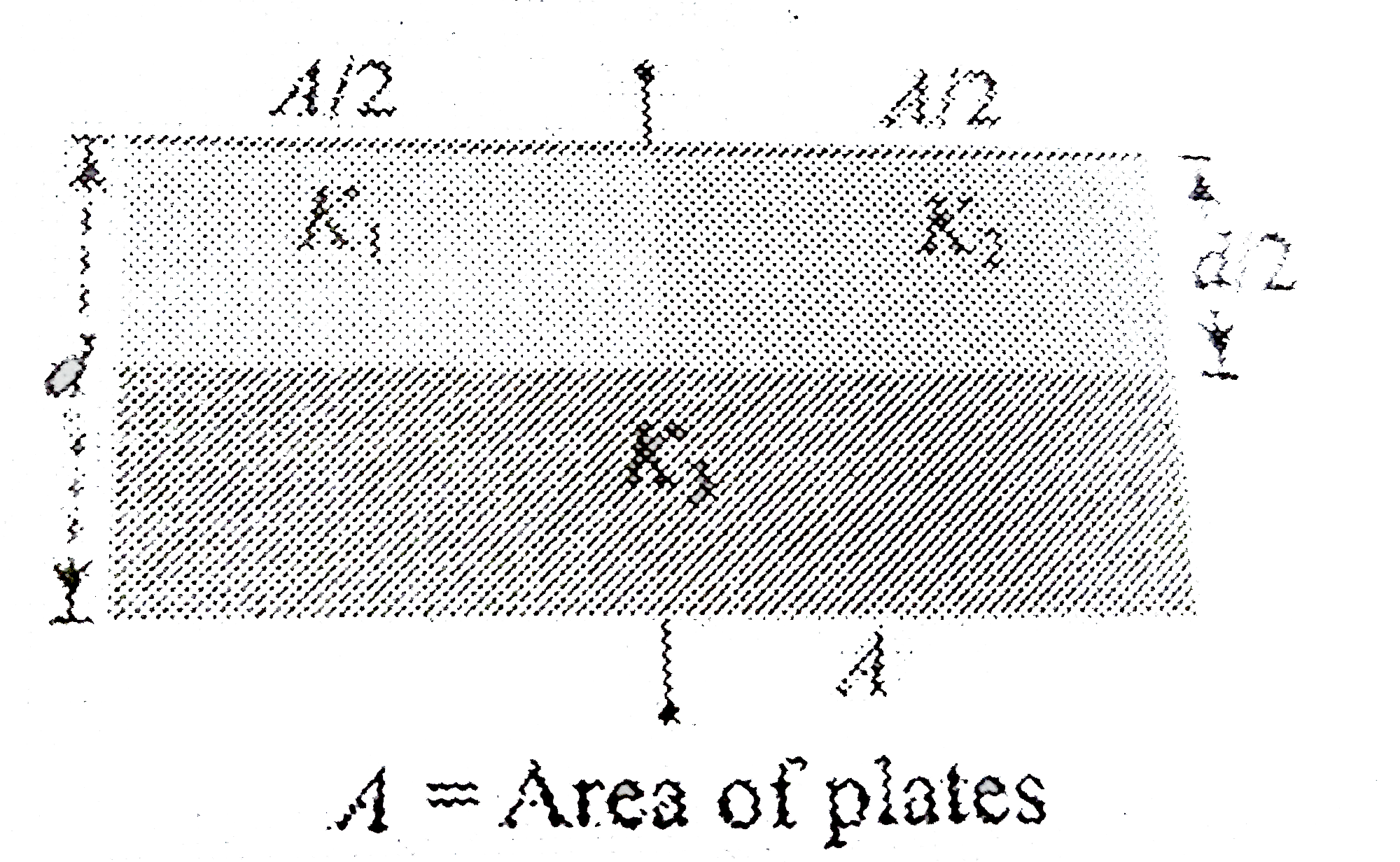 A1k=1k2+1k2+12k3B1k=1k2+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1+k2+2k3
A1k=1k2+1k2+12k3B1k=1k2+k2+12k3Ck=k1k2k1+k2+2k3Dk=k1+k2+2k3A parallel plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials hving dielectric constants K1,K2,K3 and K4 as shown in the figure below. If a single dielectric material is to be used to have the same capacitance c in this capacitor, then its dielectric constant K is given by
 AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
AK=K1+K2+K3+3K4BK=23(K1+K2+K3)+2K4C2K=3K1+K2+K3+1K4D1K=1K1+1K2+1K3+32K4
A parallel plate capacitor with plate area A & plate separation d is filled with a dielectric material of dielectric constant given byK=K0(1+αx).. Calculate capacitance of system: (given αd<<1).

View SolutionA parallel plate capacitor of area A, plate separation d and capacitance C is filled with three different dielectric materials having dielectric constants k1, k2 and k3 as shown. If a single dielectric material is to be used to have the same capacitance C in this capacitor, then its dielectic constant k is given by
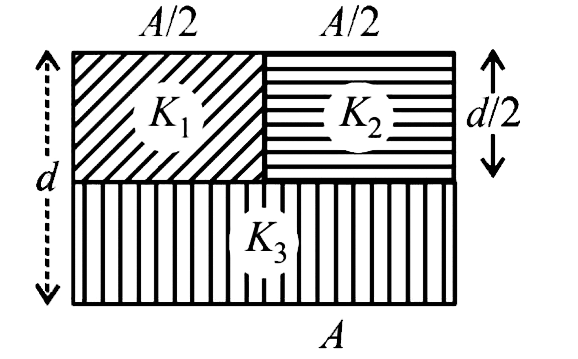
View SolutionA parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by
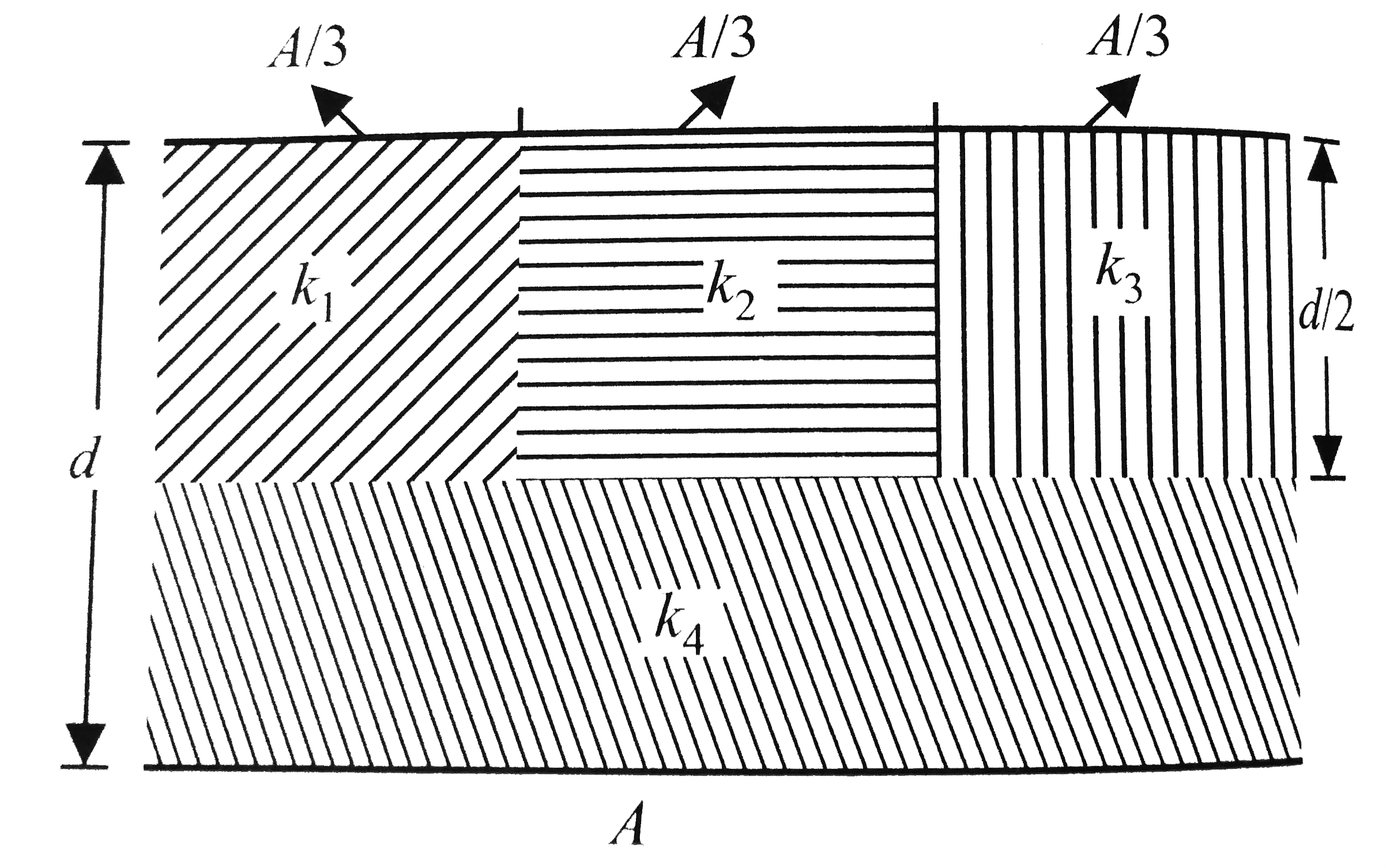
View SolutionA parallel -plate capacitor of area A, plate separation d and capacitance C is filled with four dielectric materials having dielectric constant k1,k2,k3 and k4 as shown in the figure below. If a single dielectric materical is to be used to have the same capacitance C in this capacitor, then its dielectric constant k is given by

View SolutionA parallel plate capacitor of area ‘A’ plate separation ‘d’ is filled with two dielectrics as shown. What is the capacitance of the arrangement ?

View Solution

