Let E1(r), E2(r) and E3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density λ, and an infinite plane with uniform surface charge density σ. If E1(r0)=E2(r0)=E3(r0) at a given distance r0, then
Q=4σπr20
r0=λ2πσ
E1(r0/2)=2E2(r0/2)
E2(r0/2)=4E3(r0/2)
The correct Answer is:C
Step by step video, text & image solution for Let E_1(r), E_2(r) and E_3(r) be the respectively electric field at a distance r from a point charge Q, an infinitely long wire with constant linear charge density lambda, and an infinite plane with uniform surface charge density sigma. If E_1(r_0)=E_2(r_0)=E_3(r_0) at a given distance r_0, then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Knowledge Check
Electric field at a point of distance r from a uniformly charged wire of infinite length having linear charge density λ is directly proportional to
Ar−1BrCr2Dr−2A charge particle q is released at a distance R∘ from the infinite long wire of linear charge density λ. Then velocity will be proportional to (At distance R from the wire)
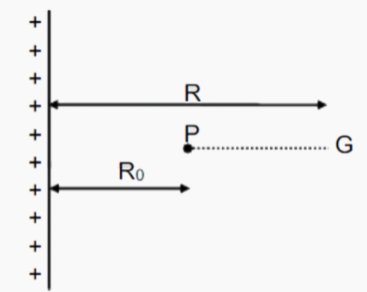 AR3BeR/R0CR2D[n(RR0)]−1/2
AR3BeR/R0CR2D[n(RR0)]−1/2For a long wire of charge density γ,, field at a distance r from the wire is
Aγ2πε0rnBγ4πε0rnC0Dkqεe
Electric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View SolutionElectric field at a point near a uniformaly charged infinite plane sheet having surface density of charge σ is given as E= ________________
View SolutionElectric field 'E' at a point situated at a normal distacne 'r' from an infinitely long uniformaly charged straight were is proportional to
View SolutionLet E1andE2 denotes gravitational field at distance r1andr2 from the axis of an infinitely long solid cylinder of the radius R. Which of the following must hold true ?
View SolutionThe electric field due to point charged at a distance R form it is E. if the same charge is placed on a metallic sphere of Radius R, the electric field on the surface of the sphere will be
View Solution
